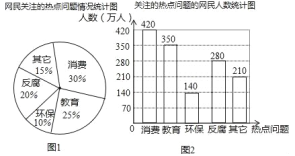
【题目】杭州某网站调查,2014年网民们最关注的热点话题分别有:消费、教育、环保、反腐及其它共五类.根据调查的部分相关数据,绘制的统计图表如下:

根据以上信息解答下列问题:
(1)请补全条形统计图并在图中标明相应数据;
(2)若杭州市约有900万人口,请你估计最关注环保问题的人数约为多少万人?
(3)在这次调查中,某单位共有甲、乙、丙、丁四人最关注教育问题,现准备从这四人中随机抽取两人进行座谈,则抽取的两人恰好是甲和乙的概率为 .
参考答案:
【答案】(1)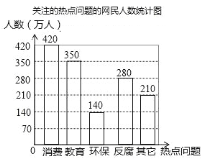 ;(2)90;(3)
;(2)90;(3)![]()
【解析】
试题分析:(1)根据关注消费的人数是420人,所占的比例式是30%,即可求得总人数,然后利用总人数乘以关注教育的比例求得关注教育的人数;(2)利用总人数乘以对应的百分比即可;(3)利用列举法即可求解即可.
试题解析:(1)调查的总人数是:420÷30%=1400(人),
关注教育的人数是:1400×25%=350(人).
 ;
;
(2)900×10%=90万人;
(3)画树形图得:

则P(抽取的两人恰好是甲和乙)=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形三边之比为3:5:7,与它相似的三角形的最长边为21cm,则其余两边之和为( )
A.24cm
B.21cm
C.13cm
D.9cm -
科目: 来源: 题型:
查看答案和解析>>【题目】【回归课本】我们曾学习过一个基本事实:两条直线被一组平行线所截,所得的对应线段成比例.
【初步体验】
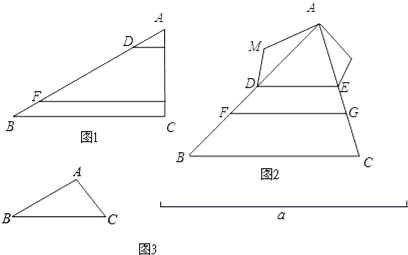
(1)如图1,在△ABC中,点D、F在AB上,E、G在AC上,DE∥FC∥BC.若AD=2,AE=1,DF=6,则EG= ,
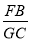 = .
= .(2)如图2,在△ABC 中,点D、F在AB上,E、G在AC上,且DE∥BC∥FG.以AD、DF、FB为边构造△ADM(即AM=BF,MD=DF);以AE、EG、GC为边构造△AEN(即AN=GC,NE=EG).
求证:∠M=∠N.
【深入探究】
上述基本事实启发我们可以用“平行线分线段成比例”解决下列问题:
(3)如图3,已知△ABC和线段a,请用直尺与圆规作△A′B′C′.
满足:①△A′B′C′∽△ABC;②△A′B′C′的周长等于线段a的长度.(保留作图痕迹,并写出作图步骤)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程:x2﹣(m﹣3)x﹣m=0.
(1)试判断原方程根的情况;
(2)若抛物线y=x2﹣(m﹣3)x﹣m与x轴交于A(x1,0),B(x2,0)两点,则A,B两点间的距离是否存在最大或最小值?若存在,求出这个值;若不存在,请说明理由.
(友情提示:AB=|x2﹣x1|)
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.

(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
(2)不改变图1中灯泡的高度,将两个边长为30cm的正方形框架按图2摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图3摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由一些完全相同的小正方体搭成的几何体的俯视图和左视图,组成这个几何体的小正方体的个数是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个锐角三角形两边长分别为3,4,则第三边长不可能的值是( )
A、4 B、2 C、6 D、4.5
相关试题

