【题目】如图,△ABC中,AB=5cm,BC=3cm,AC=4cm,若动点P从点C开始,按C→A→B的路径运动,且速度为每秒2cm,设出发的时间为t秒
(1)请判断△ABC的形状,说明理由.
(2)当t= 时,△BCP是以BC为腰的等腰三角形.
(3)另有一点Q,从点C开始,按C→B→A→C的路径运动,且速度为每秒1cm,若P、Q两点同时出发,当P、Q中有一点到达终点时,另一点也停止运动.当t为何值时,P、Q两点之间的距离为![]() ?
?

参考答案:
【答案】(1)△ABC是直角三角形,理由见解析;
(2)t=1.5或2.7或3;
(3)t=1或t=![]()
【解析】试题分析:(1)直接利用勾股定的逆定理得出△ABC是直角三角形;
(2)由于动点P从点C开始,按C→A→B的路径运动,故应分点P在AC上与AB上两种情况进行讨论;
(3)当P、Q两点之间的距离为![]() 时,分三种情况讨论:点P在AC上,点Q在BC上;点P、Q均在AB上运动,且点P在点Q的左侧;点P、Q均在AB上运动,且点P在点Q的右侧,分别求得t的值并检验即可.
时,分三种情况讨论:点P在AC上,点Q在BC上;点P、Q均在AB上运动,且点P在点Q的左侧;点P、Q均在AB上运动,且点P在点Q的右侧,分别求得t的值并检验即可.
试题解析:(1)∵AB=5,BC=3,AC=4
∴AC2+BC2= AB2
∴△ABC是直角三角形
(2)如图,当点P在AC上时,CP=CB=3,则t=3÷2=1.5秒;
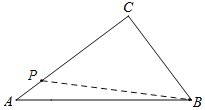
如图,当点P在AB上时,分两种情况:
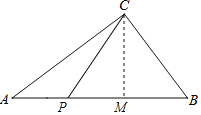
若BP=BC=3,则AP=2,
故t=(4+2)÷2=3秒;
若CP=CB=3,作CM⊥AB于M,则
![]() ×AB×MC=
×AB×MC=![]() ×BC×AC,
×BC×AC,
![]() ×5×MC=
×5×MC=![]() ×3×4,
×3×4,
解得CM=2.4,
∴由勾股定理可得PM=BM=1.8,即BP=3.6,
∴AP=1.4,
故t=(4+1.4)÷2=2.7秒.
综上所述,当t=1.5、3或2.7时,△BCP是以BC为腰的等腰三角形。
故答案为:t=1.5或2.7或3;
(3)①如图,当点P在AC上,点Q在BC上运动时(0t2),
由勾股定理可得:(2t) +t=5,
解得t=1;
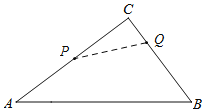
②如图,当点P、Q均在AB上运动,且点P在点Q的左侧时(3t<4),
由题可得:12-3t=![]() ,
,
解得t=![]() ;
;
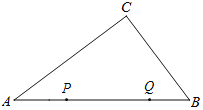
③当点P、Q均在AB上运动,且点P在点Q的右侧时(4<t4.5),
由题可得:2t+t12=![]() ,
,
解得t=![]() ,
,
∵t=![]() >4.5,
>4.5,
∴不成立,舍去.
综上所述,当t为1秒或![]() 秒时,P、Q两点之间的距离为
秒时,P、Q两点之间的距离为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示1306000应记作_______________;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为a,在AB、BC、CD、DA边上分别取点A1、B1、C1、D1,使AA1=BB1=CC1=DD1=
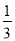 a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=
a,在边A1B1、B1C1,C1D1、D1A1上分别取点A2、B2、C2、D2,使A1A2、B1B2、C1C2、D1D2=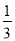 A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )
A1B1,…,依次规律继续下去,则正方形AnBnCnDn的面积为( )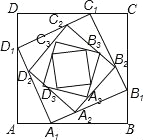
A.
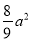 B.(
B.(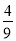 )na2 C.(
)na2 C.(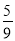 )n-1a2 D.(
)n-1a2 D.(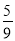 )na2
)na2 -
科目: 来源: 题型:
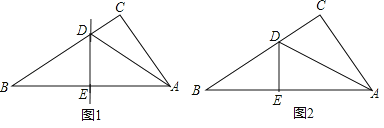
查看答案和解析>>【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
(1)如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE,若AC=6cm,BC=8cm,求CD的长.
(2)如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=6cm,BC=8cm,求CD的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+2x–m=0有实数解,那么m的取值范围是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)中日钓鱼岛争端持续,我海监船加大钓鱼岛附近海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.

(1)请用直尺和圆规作出C处的位置;
(2)求我国海监船行驶的航程BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△AOB是直角三角形,∠AOB=90°,OB=2OA,点A在反比例函数y=
 的图象上.若点B在反比例函数y=
的图象上.若点B在反比例函数y=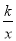 的图象上,则k的值为( )
的图象上,则k的值为( )
A.-4 B.4 C.-2 D.2
相关试题

