【题目】我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.
(1)写出你所学过的特殊四边形中是勾股四边形的一种图形的名称 ;
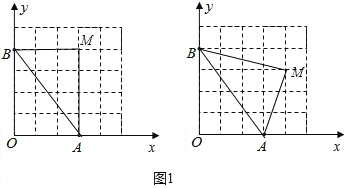
(2)如图 1,已知格点(小正方形的顶点)O(0,0),A(3,0),B(0,4),请你直接写出所有以格点为顶点,OA、OB 为勾股边且有对角线相等的勾股四边形 OAMB 的顶点M 的坐标: ;
(3)如图 2,将△ABC 绕顶点 B 按顺时针方向旋转 60°,得到△DBE,连接 AD、DC,∠DCB=30°.求证: DC2 BC2 AC2 ,即四边形 ABCD 是勾股四边形;
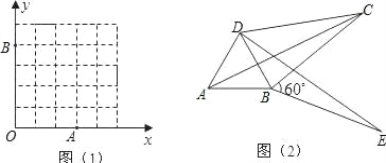
(4)若将图 2 中△ABC 绕顶点 B 按顺时针方向旋转 a 度(0°<a <90°),得到△DBE,连接 AD、DC,则当∠DCB= °时,四边形BECD 是勾股四边形.
参考答案:
【答案】(1)矩形(正方形);(2)M(3,4);M(4,3);(3)详见解析;(4)![]() α.
α.
【解析】
(1)根据勾股四边形的定义,可知正方形、矩形直角梯形都是勾股四边形;
(2)如图1中,以OA、OB为勾股边且有对角线相等的勾股四边形OAMB的顶点M的坐标为(3,4)或(4,3);
(3)如图2,连接CE,只要证明△DCE是直角三角形即可解决问题.
(4)如图3,当∠DCB= ![]() α,四边形ABCD是勾股四边形.连接CE,根据△DCE是直角三角形求出∠DCB即可.
α,四边形ABCD是勾股四边形.连接CE,根据△DCE是直角三角形求出∠DCB即可.
(1)矩形(正方形)
(2)M(3,4);M(4,3)
(3)连接CE,∵△ABC≌△DBE,∴AC=DE,BC=BE
∵∠CBE=60°,∴△CBE是等边三角形,
∴BC=BE,∠CBE=60°,∵∠DCB=30°
∴∠DCE=90°,∴DC2+EC2=DE2
∴DC2+BC2=AC2,即四边形ABCD是勾股四边形.

(4)如图 3, 当 ∠DCB=![]() α ,四边形 ABCD 是勾股四边形.
α ,四边形 ABCD 是勾股四边形.
理由:连接 CE ,

由旋转得: △ABC ≌ △DBE ,
∴AC=DE , BC=BE ,
又 ∵∠CBE=α ,
∴∠BCE=∠BEC=90°![]() α ,
α ,
∴当∠DCB=![]() α时,∠DCE=90° ,
α时,∠DCE=90° ,
∴DC2+EC2=DE2 .
∴ 即四边形BECD 是勾股四边形
故答案为:![]() α.
α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,方格图中每个小正方形的边长为1,点A、B、C都是格点.
(1)画出△ABC关于直线MN对称的△A1B1C1;
(2)直接写出AA1的长度;
(3)如图2,A、C是直线MN同侧固定的点,D是直线MN上的一个动点,在直线MN上画出点D,使AD+DC最小.(保留作图痕迹)

-
科目: 来源: 题型:
查看答案和解析>>【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养,随机抽取了部分学生对这三项活动的兴趣情况进行了调查(每人从中只能选一项),并将调查结果绘制成如图两幅统计图,请你结合图中信息解答问题.
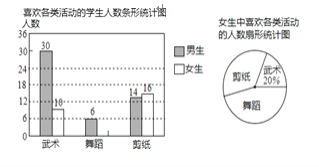
(1)将条形统计图补充完整;
(2)本次抽样调查的样本容量是 ;
(3)已知该校有1200名学生,请你根据样本估计全校学生中喜欢剪纸的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图中是抛物线型拱桥,P处有一照明灯,水面OA宽4m,从O,A两处观测P处,仰角分别为α,β,tanα=
 ,tanβ=
,tanβ= ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系.(1)求点P的坐标;
(2)水面上升1m,水面宽多少(
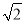 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?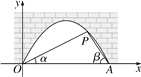
-
科目: 来源: 题型:
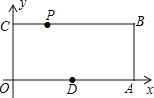
查看答案和解析>>【题目】已知,如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B 运动.设 动点P的运动时间为t秒
(1)当t为何值时,四边形PODB是平行四边形?
(2)在直线CB上是否存在一点Q,使得O、D、Q、P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由。
(3) 在线段PB上有一点M,且PM=5,当P运动 秒时,四边形OAMP的周长最小, 并画图标出点M的位置。

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN.

相关试题

