【题目】某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图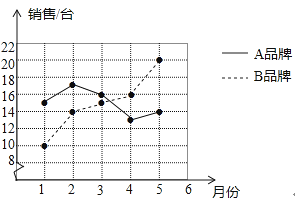
(1)分别求该商场这段时间内A,B两种品牌冰箱月销售量的中位数和方差。
(2)根据计算结果,比较该商场1~5月这两种品牌冰箱月销售量的稳定性。
参考答案:
【答案】
(1)
解:(1)A品牌冰箱月销售量从小到大的排列为:13,14,15,16,17,
B品牌冰箱月销售量从小到大排列为:10,14,15,16,20,
∴A品牌冰箱月销售量的中位数为15台,B品牌冰箱月销售量的中位数为15台,
∵![]() =
=![]() =15(台);
=15(台);![]() =
=![]() =15(台),
=15(台),
则SA2=![]() =2,SB2=
=2,SB2=![]() =10.4;
=10.4;
(2)
解∵SA2<SB2,
∴A品牌冰箱的月销售量稳定。
【解析】(1)根据折线统计图得出A,B两种品牌冰箱的销售台数,分别求出中位数与方差即可;
(2)根据(1)的结果比较即可得到结果.
此题考查了统计图的应用,涉及知识点有折线统计图,中位数和方差等。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△DBC是两个具有公共边的全等三角形,AB=AC=3cm.BC=2cm,将△DBC沿射线BC平移一定的距离得到△D1B1C1 , 连接AC1 , BD1 . 如果四边形ABD1C1是矩形,那么平移的距离为 cm.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
 ﹣(
﹣( ﹣π)0﹣2
﹣π)0﹣2 sin60°
sin60°
(2)化简:(1+ )
) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)解方程:
 =
= ;
;
(2)解不等式组:
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.
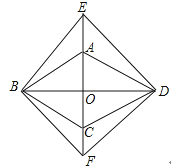
(1)求证:△BAE≌△BCF
(2)若∠ABC=50°,则当∠EBA=°时,四边形BFDE是正方形. -
科目: 来源: 题型:
查看答案和解析>>【题目】活动1:
在一只不透明的口袋中装有标号为1,2,3的3个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三位同学丙→甲→乙的顺序依次从袋中各摸出一个球(不放回),摸到1号球胜出,计算甲胜出的概率.(注:丙→甲→乙表示丙第一个摸球,甲第二个摸球,乙最后一个摸球)
(1)活动1:
在一只不透明的口袋中装有标号为1,2,3的3个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三位同学丙→甲→乙的顺序依次从袋中各摸出一个球(不放回),摸到1号球胜出,计算甲胜出的概率.(注:丙→甲→乙表示丙第一个摸球,甲第二个摸球,乙最后一个摸球)
(2)活动2:
在一只不透明的口袋中装有标号为1,2,3,4的4个小球,这些球除标号外都相同,充分搅匀,请你对甲、乙、丙三名同学规定一个摸球顺序:→→ , 他们按这个顺序从袋中各摸出一个球(不放回),摸到1号球胜出,则第一个摸球的同学胜出的概率等于 ,最后一个摸球的同学胜出的概率等于
(3)猜想:
在一只不透明的口袋中装有标号为1,2,3,…,n(n为正整数)的n个小球,这些球除标号外都相同,充分搅匀,甲、乙、丙三名同学从袋中各摸出一个球(不放回),摸到1号球胜出,猜想:这三名同学每人胜出的概率之间的大小关系.
你还能得到什么活动经验?(写出一个即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形﹣正八边形.

(1)如图②,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹);
(2)在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于
相关试题

