【题目】如图,四边形AOBC是正方形,OA=4,动点P从点O出发,沿折线OACB方向以1个单位/秒的速度匀速运动,另一个点Q从O出发,沿折线OBCA方向以2个单位/秒的速度匀速运动,运动时间为t秒,当它们相遇时停止运动,当以A、P、B、Q四点为顶点的四边形为平行四边形时,t的值为______.

参考答案:
【答案】![]()
【解析】
根据正方形的性质求出正方形的边长,再根据以A,P,B,Q四点为顶点的四边形是平行四边形可知,只有点P在OA上,点Q在BC上时符合,根据平行四边形的对边相等,分别表示出AP与BQ的长度,然后求解即可.
∵四边形AOBC是正方形,∴AO=AC,在RT△AOC中,OC=![]() ,
,
∴点C的坐标是(4![]() ,0),
,0),
∵P和Q运动到相遇时停止,且Q的运动速度比P快,正方形的边长是4,
∴只有点P在OA上,点Q在BC上时符合题意,如图所示,
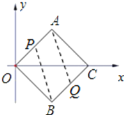
此时,AP=4-t,BQ=2t-4,
∵四边形APBQ是平行四边形,
∴AP=BQ,
∴4-t=2t-4,
解得t=![]() .
.
故答案为:![]() 秒.
秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读理解)
点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C到B的距离3倍,那么我们就称点C是{A,B}的奇点.
例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇点.
(知识运用)
如图2,M、N为数轴上两点,点M所表示的数为﹣3,点N所表示的数为5.
(1)数 所表示的点是{M,N}的奇点;数 所表示的点是{N,M}的奇点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣50,点B所表示的数为30.现有一动点P从点B出发向左运动,当P点运动到数轴上的什么位置时,P、A和B中恰有一个点为其余两点的奇点?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的边AB是⊙O的弦.
(1)如图1,若AB是⊙O的直径,AB=AC,BC交⊙O于点D,且DM⊥AC于M,请判断直线DM与⊙O的位置关系,并给出证明;
(2)如图2,AC交⊙O于点E,若E恰好是
 的中点,点E到AB的距离是8,且AB长为24,求⊙O的半径长.
的中点,点E到AB的距离是8,且AB长为24,求⊙O的半径长.
-
科目: 来源: 题型:
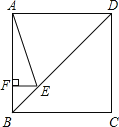
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,点E对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长为( )
A. 1B. 4-
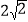 C.
C. 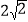 D.
D.  -4
-4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=﹣x2+mx+n交x轴于点A(﹣2,0)和点B,交y轴于点C(0,2).
(1)求抛物线的函数表达式;
(2)若点M在抛物线上,且S△AOM=2S△BOC,求点M的坐标;
(3)如图2,设点N是线段AC上的一动点,作DN⊥x轴,交抛物线于点D,求线段DN长度的最大值.
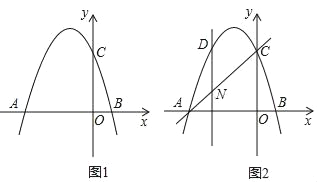
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)(﹣63)+17+(﹣23)+68;
(2)3
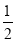 +(﹣
+(﹣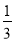 )+(﹣3
)+(﹣3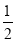 )+2
)+2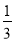 ;
;(3)
 ;
;(4)
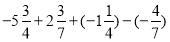
-
科目: 来源: 题型:
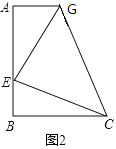
查看答案和解析>>【题目】(1)如图,在正方形ABCD中,E是AB上一点,G是AD上一点,∠ECG=45°,那么EG与图中两条线段的和相等?证明你的结论.
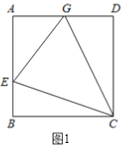
(2)请用(1)中所积累的经验和知识完成此题,如图,在四边形ABCG中,AG//BC(BC>AG),∠B=90°,AB=BC=12,E是AB上一点,且∠ECG=45°,BE=4,求EG的长?
相关试题

