【题目】如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
参考答案:
【答案】
(1)解:E(3,1);F(1,2).
(2)解:在Rt△EBF中,∠B=90°,
∴EF= ![]() .
.
设点P的坐标为(0,n),其中n>0,
∵顶点F(1,2),
∴设抛物线解析式为y=a(x﹣1)2+2(a≠0).
① 如图1,
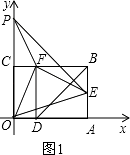
当EF=PF时,EF2=PF2,
∴12+(n﹣2)2=5.
解得n1=0(舍去);n2=4.
∴P(0,4).
∴4=a(0﹣1)2+2.
解得a=2.
∴抛物线的解析式为y=2(x﹣1)2+2
② 如图2,
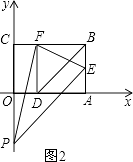
当EP=FP时,EP2=FP2,
∴(2﹣n)2+1=(1﹣n)2+9.
解得 ![]() (舍去)
(舍去)
③当EF=EP时,EP= ![]() ,这种情况不存在.
,这种情况不存在.
综上所述,符合条件的抛物线解析式是y=2(x﹣1)2+2.
(3)解:存在点M,N,使得四边形MNFE的周长最小.
如图3,作点E关于x轴的对称点E′,作点F关于y轴的对称点F′, 
连接E′F′,分别与x轴、y轴交于点M,N,则点M,N就是所求点.
∴E′(3,﹣1),F′(﹣1,2),NF=NF′,ME=ME′.
∴BF′=4,BE′=3.
∴FN+NM+ME=F′N+NM+ME′=E′F′= ![]() .
.
又∵ ![]() ,
,
∴FN+MN+ME+EF=5+ ![]() ,此时四边形MNFE的周长最小值是
,此时四边形MNFE的周长最小值是 ![]() .
.
【解析】(1)首先依据翻折的性质可证明四边形ADFB是正方形,故此可得到BF=AB=OC=2,则CF=3-2=1,因而E、F的坐标就可以求出;
(2)由抛物线的顶点坐标为(1,2),故此可设抛物线的解析式为y=a(x-1)2+2,然后分为以下三角形情况进行解答即可:当EF是腰,EF=PF时,已知E、F点的坐标可以求出EF的长,设P点的坐标是(0,n),根据勾股定理就可以求出n的值.得到P的坐标.当EF是腰,EF=EP时,可以判断E到y轴的最短距离与EF的大小关系,只有当EF大于E到y轴的距离,P才存在.当EF是底边时,EP=FP,根据勾股定理就可以得到关于n的方程,就可以解得n的值.
(3)作点E关于x轴的对称点E′,作点F关于y轴的对称点F′,依据轴对称图形的性质可得到NF=NF′,ME=ME′,然后依据两点之间线段最短可得到FN+NM+ME的最小值等于E′F′,故此可得到四边形MNFE的周长的最小值.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个三棱柱包装盒,它的底面是边长为10cm的正三角形,三个侧面都是矩形.现将宽为15cm的彩色矩形纸带AMCN裁剪成一个平行四边形ABCD(如图2),然后用这条平行四边形纸带按如图3的方式把这个三棱柱包装盒的侧面进行包贴(要求包贴时没有重叠部分),纸带在侧面缠绕三圈,正好将这个三棱柱包装盒的侧面全部包贴满.在图3中,将三棱柱沿过点A的侧棱剪开,得到如图4的侧面展开图.为了得到裁剪的角度,我们可以根据展开图拼接出符合条件的平行四边形进行研究.
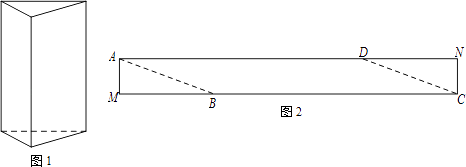
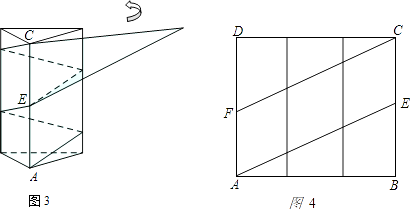
(1)请在图4中画出拼接后符合条件的平行四边形;
(2)请在图2中,计算裁剪的角度(即∠ABM的度数). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,一次函数y=kx+3的图象经过点A(1,4).
(1)求这个一次函数的解析式;
(2)试判断点B(-1,5),C(0,3),D(2,1)是否在这个一次函数的图象上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知直线
 的图象与x轴、y轴交于A,B两点,直线
的图象与x轴、y轴交于A,B两点,直线 经过原点,与线段AB交于点C,把
经过原点,与线段AB交于点C,把 的面积分为2:1的两部分,求直线
的面积分为2:1的两部分,求直线 的解析式.
的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD相交于O,EF过点O与AD,BC分别相交于E,F,若AB=4,BC=5,OE=1.5,那么四边形EFCD的周长为( )

A.16
B.14
C.12
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD边长为4,点P从点A运动到点B,速度为1,点Q沿B﹣C﹣D运动,速度为2,点P、Q同时出发,则△BPQ的面积y与运动时间t(t≤4)的函数图象是( )

A.
B.
C.
D.
相关试题

