【题目】如图,四边形ABCD的对角线交于点O,AB∥CD,O是BD的中点.
(1)求证:△ABO≌△CDO;
(2)若BC=AC=4,BD=6,求△BOC的周长.

参考答案:
【答案】(1)见解析;(2)9
【解析】
(1)根据平行线性质得出∠A=∠C,∠D=∠B,根据AAS推出即可;
(2)根据全等三角形的性质得到AO=OC=![]() AC=2,根据三角形的周长的公式即可得到结论.
AC=2,根据三角形的周长的公式即可得到结论.
(1)证明:∵AB∥CD,
∴∠BAC=∠ACD,∠ABD=∠CDB.
又∵O是BD的中点,
∴OB=OD.
在△ABO和△CDO中,∵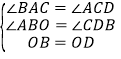
∴△ABO≌△CDO(AAS).
(2)∵△ABO≌△CDO,AC=4,
∴AO=OC=![]() AC=2.
AC=2.
∵O是BD的中点,BD=6,
∴OB=![]() BD=3,
BD=3,
∴△BOC的周长=BC+OB+OC=4+3+2=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校要求八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:
八年级2班参加球类活动人数统计表
项目
篮球
足球
乒乓球
排球
羽毛球
人数
a
6
5
7
6
根据图中提供的信息,解答下列问题:
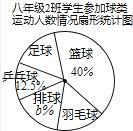
(1)a= , b=
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约人;
(3)该班参加乒乓球活动的5位同学中,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=CB,BE=BF,点A,B,C在同一条直线上,∠1=∠2.
(1)证明:△ABE≌△CBF;
(2)若∠FBE=40°,∠C=45°,求∠E的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年“母亲节”前夕,宜宾某花店用4000元购进若干束花,很快售完,接着又用4500元购进第二批花,已知第二批所购花的束数是第一批所购花束数的1.5倍,且每束花的进价比第一批的进价少5元
(1)求第一批花每束的进价是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】(2017·河北迁安一模)如图,在Rt△ABC中,直角边AC=7 cm,BC=3 cm,CD为斜边AB上的高,点E从点B出发沿直线BC以2 cm/s的速度移动,过点E作BC的垂线交直线CD于点F.
(1)试说明:∠A=∠BCD;
(2)点E运动多长时间,CF=AB?并说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2018的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
相关试题

