【题目】解下列方程
(1)x2+3x=0
(2)49=x2﹣2x﹣50(用配方法解)
参考答案:
【答案】
(1)解:x2+3x=0
x(x+3)=0
x=0,x+3=0
x1=0,x2=﹣3
(2)解:49=x2﹣2x﹣50
x2﹣2x+1=100
(x﹣1)2=100
x﹣1=±10
x1=11,x2=﹣9
【解析】(1)利用因式分解法解方程; (2)利用配方法解方程.
【考点精析】通过灵活运用配方法和因式分解法,掌握左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题;已知未知先分离,因式分解是其次.调整系数等互反,和差积套恒等式.完全平方等常数,间接配方显优势即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断对错:轴对称图形也是中心对称图形;__________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】指出下列命题的条件和结论.
(1)一个锐角的补角大于这个角的余角;
(2)不相等的两个角不是对顶角;
(3)异号两数相加得零.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2-2x+k=0.
(1)若方程有实数根,求k的取值范围;
(2)如果k是满足条件的最大的整数,且方程x2-2x+k=0一根的相反数是一元二次方程(m-1)x2-3mx-7=0的一个根,求m的值及这个方程的另一根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD、BEFG均为正方形,连接AG、CE.
(1)求证:AG=CE;
(2)求证:AG⊥CE.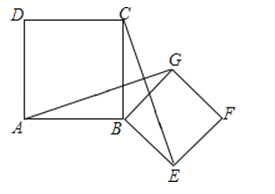
-
科目: 来源: 题型:
查看答案和解析>>【题目】判断对错:对顶角是中心对称图形;________________
相关试题

