【题目】我们知道，与三角形各边都相切的圆叫做三角形的内切圆，则三角形可以称为圆的外切三角形．如图1，与的三边分别相切于点则叫做的外切三角形.以此类推，各边都和圆相切的四边形称为圆外切四边形．如图2，与四边形ABCD的边分别相切于点则四边形叫做的外切四边形．

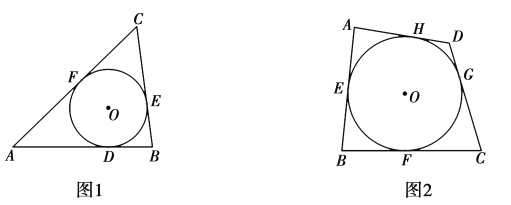
（1）如图2，试探究圆外切四边形的两组对边与之间的数量关系，猜想： (横线上填“>”，“<”或“=”)；

（2）利用图2证明你的猜想(写出已知，求证，证明过程)；

（3）用文字叙述上面证明的结论： ；

（4）若圆外切四边形的周长为相邻的三条边的比为，求此四边形各边的长．

【答案】（1）=；（2）答案见解析；（3）圆外切四边形的对边之和相等；（4）4；10；12；6

【解析】

（1）根据圆外切四边形的定义猜想得出结论；
（2）根据切线长定理即可得出结论；
（3）由（2）可得出答案；
（4）根据圆外切四边形的性质求出第四边，利用周长建立方程求解即可得出结论．

解：（1）∵⊙O与四边形ABCD的边AB，BC，CD，DA分别相切于点E，F，G，H，
∴猜想AB+CD=AD+BC，
故答案为：=．

已知:四边形的四边分别与相切于点

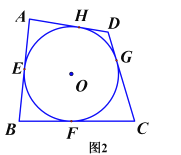
求证:

证明:与相切，

同理:

由（2）可知：圆外切四边形的对边和相等．
故答案为：圆外切四边形的对边和相等；

解:相邻的三条边的比为，

设此三边为

根据圆外切四边形的性质得:第四边的长为:

圆外切四边形的周长为，

解得

此四边形的四边长分别为:.

关闭