【题目】如图,EF∥AD,∠1=∠2.说明:∠DGA+∠BAC=180°.请将说明过程填写完成.
解:∵EF∥AD,(已知)
∴∠2= . ()
又∵∠1=∠2,()
∴∠1=∠3,()
∴AB∥ , ()
∴∠DGA+∠BAC=180°.()
参考答案:
【答案】∠3;两直线平行,同位角相等;已知;等量代换;DG;内错角相等,两直线平行;两直线平行,同旁内角互补
【解析】解:∵EF∥AD,(已知)
∴∠2=∠3.(两直线平行,同位角相等)
又∵∠1=∠2,(已知)
∴∠1=∠3,(等量代换)
∴AB∥DG,(内错角相等,两直线平行)
∴∠DGA+∠BAC=180°(两直线平行,同旁内角互补).
【考点精析】掌握平行线的判定与性质是解答本题的根本,需要知道由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(m+2)x+m2﹣4是一次函数,则m .
-
科目: 来源: 题型:
查看答案和解析>>【题目】教育行政部门规定初中生每天户外活动的平均时间不少于1小时,为了解学生户外活动的情况,随机地对部分学生进行了抽样调查,并将调查结果绘制成如下两幅不完整的统计图.请根据图中提供的信息解答下列问题:
(1)在这次调查中共调查的学生人数为 .
(2)若我市共有初中生约14000名,试估计我市符合教育行政部门规定的活动时间的学生数;
(3)试通过对抽样数据的分析计算,说明我市初中生参加户外活动的平均时间是否符合教育行政部门的要求?

-
科目: 来源: 题型:
查看答案和解析>>【题目】□ABCD中,∠A:∠B=1:2,则∠C的度数为( ).
A. 30° B. 45° C. 60° D. 120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式mx+n可分解为m(x-y),则n表示的整式为( )
A. m B. my C. -y D. -my
-
科目: 来源: 题型:
查看答案和解析>>【题目】“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若m、n(m<n)是关于x的方程1﹣(x﹣a)(x﹣b)=0的两根,且a<b,则a、b、m、n的大小关系是( ).
A.
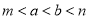 B.
B. 
C.
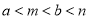 D.
D. 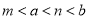
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1)。

(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍画出图形。
(2)写出B、C两点的对应点B、C的坐标;
(3)如果△OBC内部一点M的坐标为(x,y),写出M的对应点M的坐标。
相关试题

