【题目】已知抛物线的顶点为(1,﹣3),且过点(2,1),求这个函数的表达式为________.
参考答案:
【答案】y=4x2﹣8x+1
【解析】
因为抛物线的顶点为(1,-3),可设抛物线的解析式为y=a(x-1)2-3,把(2,1)代入解析式可求a,从而确定这个函数的表达式.
设抛物线的解析式为y=a(x-1)2-3,
把点(2,1)代入解析式得:a-3=1,
解得a=4,
∴这个函数的表达式为y=4(x-1)2-3,
即y=4x2-8x+1.
故答案为y=4x2-8x+1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学很多的知识都是以发明者的名字命名的,如韦达定理、杨辉三角、费马点等,你知道平面直角坐标系是哪一位法国的数学家创立的,并以他的名字命名的吗?( )
A. 迪卡尔 B. 欧几里得 C. 欧拉 D. 丢番图
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点M的坐标为(-2,-3),则点M关于原点对称的坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生参加社团的情况,从2010年起,某市教育部门每年都从全市所有学生中随机抽取2000名学生进行调查,图①、图②是部分调查数据的统计图(参加社团的学生每人只能报一项)根据统计图提供的信息解决下列
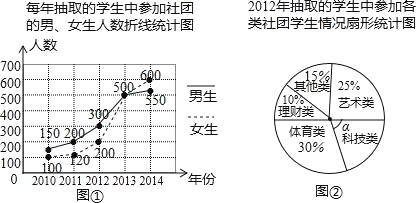
问题:
(1)求图②中“科技类”所在扇形的圆心角α的度数
(2)该市2012年抽取的学生中,参加体育类与理财类社团的学生共有多少人?
(3)该市2014年共有50000名学生,请你估计该市2014年参加社团的学生人数.
-
科目: 来源: 题型:
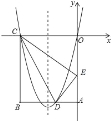
查看答案和解析>>【题目】如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求OE的长及经过O,D,C三点抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示数5.002×104 , 则原数是( )
A.5002
B.50020
C.500200
D.5002000 -
科目: 来源: 题型:
查看答案和解析>>【题目】某大型广场要举办一次能容纳10万人的演出,假设每把椅子所占面积相当于一张单人的学生课桌面积,则这个大型广场的面积约为( )
A. 2.5×106m2 B. 2.5×105m2 C. 2.5×104m2 D. 2.5×103m2
相关试题

