【题目】某商场经营某种品牌的童装,购进时的单价是60元.根据市场调查,在一段时间内,销售单价是80元时,销售量是200件,而销售单价每降低1元,就可多售出20件.
(1)写出销售量y件与销售单价x元之间的函数关系式;
(2)写出销售该品牌童装获得的利润w元与销售单价x元之间的函数关系式;
(3)若童装厂规定该品牌童装销售单价不低于76元,且商场要完成不少于240件的销售任务,则商场销售该品牌童装获得的最大利润是多少?
参考答案:
【答案】(1)销售量y件与销售单价x元之间的函数关系式为y=﹣20x+1800(60≤x≤80);
(2)销售该品牌童装获得的利润w元与销售单价x元之间的函数关系式W=﹣20x2+3000x﹣108000;
(3)所以商场销售该品牌童装获得的最大利润是4480元.
【解析】
试题分析:(1)销售量y件为200件加增加的件数(80﹣x)×20;
(2)利润w等于单件利润×销售量y件,即W=(x﹣60)(﹣20x+1800),整理即可;
(3)先利用二次函数的性质得到w=﹣20x2+3000x﹣108000的对称轴为x=﹣![]() =75,而﹣20x+1800≥240,x≤78,得76≤x≤78,根据二次函数的性质得到当76≤x≤78时,W随x的增大而减小,把x=76代入计算即可得到商场销售该品牌童装获得的最大利润.
=75,而﹣20x+1800≥240,x≤78,得76≤x≤78,根据二次函数的性质得到当76≤x≤78时,W随x的增大而减小,把x=76代入计算即可得到商场销售该品牌童装获得的最大利润.
试题解析:(1)根据题意得,y=200+(80﹣x)×20
=﹣20x+1800,
所以销售量y件与销售单价x元之间的函数关系式为y=﹣20x+1800(60≤x≤80);
(2)W=(x﹣60)y
=(x﹣60)(﹣20x+1800)
=﹣20x2+3000x﹣108000,
所以销售该品牌童装获得的利润w元与销售单价x元之间的函数关系式W=﹣20x2+3000x﹣108000;
(3)根据题意得,﹣20x+1800≥240,解得x≤78,∴76≤x≤78,
w=﹣20x2+3000x﹣108000,对称轴为x=﹣![]() =75,∵a=﹣20<0,
=75,∵a=﹣20<0,
∴抛物线开口向下,∴当76≤x≤78时,W随x的增大而减小,
∴x=76时,W有最大值,最大值=(76﹣60)(﹣20×76+1800)=4480(元).
所以商场销售该品牌童装获得的最大利润是4480元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于 x 的一元二次方程(m﹣1)x2+5x+m2﹣3m+2=0的一个根是0,则m的值是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是必然事件的为( )
A.3天内会下雨
B.打开电视,正在播放广告
C.367人中至少有2人公历生日相同
D.某妇产医院里,下一个出生的婴儿是女孩
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列长度的各组线段中,能组成三角形的是( )
A.1,2,4B.1,4,9C.3,4,5D.4,5,9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,△OBC的顶点分别为O(0,0),B(3,﹣1)、C(2,1).
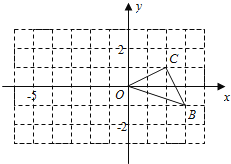
(1)以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′,画出△OB′C′,并写出点B′、C′的坐标:B′( , ),C′( , );
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标( , ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中错误的是( )
A.将油滴入水中,油会浮出水面是一个必然事件
B.1、2、3、4这组数据的中位数是2.5
C.一组数据的方差越小,这组数据的稳定性越差
D.要了解某种灯管的使用寿命,一般采用抽样调查
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2﹣2x=5,则代数式2x2﹣4x﹣1的值为___________.
相关试题

