【题目】如图,抛物线y=![]() x2+bx+c与y轴交于点C(0,-6),与x轴交于点A,B,且B点的坐标为(3,0).
x2+bx+c与y轴交于点C(0,-6),与x轴交于点A,B,且B点的坐标为(3,0).

(1)求该抛物线的解析式.
(2)若点P是AB上的一动点,过点P作PE∥AC,交BC于E,连接CP,求△PCE面积的最大值.
(3)若点D为OA的中点,点M是线段AC上一点,且△OMD为等腰三角形,求M点的坐标.
参考答案:
【答案】(1) y=![]() x2+x-6;(2)最大值为
x2+x-6;(2)最大值为![]() .(3)(-3,-3)或(-
.(3)(-3,-3)或(-![]() ,-
,-![]() ).
).
【解析】
试题分析:(1)把B点和C点坐标分别代入y=![]() x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
(2)首先求出△PCE面积的表达式,然后利用二次函数的性质求出其最大值;
(3)分三种情况进行讨论即可.
试题解析:(1)把点C(0,-6),B(3,0)分别代入y=![]() x2+bx+c中,
x2+bx+c中,
得b=1,c=-6,∴该抛物线的解析式为y=![]() x2+x-6
x2+x-6
(2)令y=0,即![]() x2+x-6=0解得x1=-6,x2=3,∴A(-6,0),S△ABC=
x2+x-6=0解得x1=-6,x2=3,∴A(-6,0),S△ABC=![]() AB×OC=27.
AB×OC=27.
设P点坐标为(x,0),则PB=3-x.∵PE∥AC,
∴∠BPE=∠BAC,∠BEP=∠BCA,∴△PBE∽△BAC,
∴![]() ,得S△PBE=
,得S△PBE=![]() (3-x)2.
(3-x)2.
S△PCE=S△PCB-S△PBE=![]() PB×OC-S△PBE=
PB×OC-S△PBE=![]() ×(3-x)×6-
×(3-x)×6-![]() (3-x)2
(3-x)2
=-![]() (x+
(x+![]() )2+
)2+![]()
∴当x=-![]() 时,S△PCE的最大值为
时,S△PCE的最大值为![]() .
.
(3)△OMD为等腰三角形,可能有三种情形:
(I)当DM=DO时,如答图①所示.DO=DM=DA=3,

∴∠OAC=∠AMD=45°,∴∠ADM=90°,
∴M点的坐标为(-3,-3);
(II)当MD=MO时,如答图②所示.

过点M作MN⊥OD于点N,则点N为OD的中点,
∴DN=ON=![]() ,AN=AD+DN=
,AN=AD+DN=![]() ,又△AMN为等腰直角三角形,
,又△AMN为等腰直角三角形,
∴MN=AN=![]() ,∴M点的坐标为(-
,∴M点的坐标为(-![]() ,-
,-![]() );
);
(III)当OD=OM时,∵△OAC为等腰直角三角形,
∴点O到AC的距离为![]() ×6=3
×6=3![]() ,即AC上的点与点O之间的最小距离为3
,即AC上的点与点O之间的最小距离为3![]() .
.
∵3![]() >3,∴OD=OM的情况不存在.
>3,∴OD=OM的情况不存在.
综上所述,点M的坐标为(-3,-3)或(-![]() ,-
,-![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,不能判定两个直角三角形全等的是( )
A.两条直角边对应相等
B.斜边和一个锐角对应相等
C.斜边和一条直角边对应相等
D.一条直角边和一个锐角分别相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】陵前街道有一家拉面馆,味道很美.你知道拉面是怎样做的吗?一根拉一次变成2根,再拉一次变成4根,在拉一次变成8根,照这样做下去,拉上10次后,拉面师傅手中的拉面有___________根
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树的正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2米,台阶AC的坡度为1:
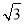 (即AB:BC=1:
(即AB:BC=1: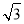 ),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).
),且B、C、E三点在同一条直线上.请根据以上条件求出树DE的高度(侧倾器的高度忽略不计).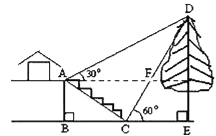
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AO
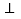 OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF.等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为_________.
OM,OA=4,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF.等腰Rt△ABE,连接EF交OM于P点,当点B在射线OM上移动时,则PB的长度为_________. 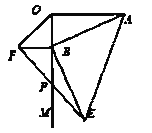
-
科目: 来源: 题型:
查看答案和解析>>【题目】我区积极开展“体育大课间”活动,引导学生坚持体育锻炼.某校根据实际情况,决定主要开设A:乒乓球,B:篮球,C:跑步,D:足球四种运动项目.为了解学生最喜欢哪一种项目,随机抽取了部分学生进行调查,并将调查结果绘制成如下统计图.请你结合图中信息解答下列问题:
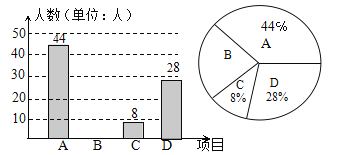
(1)求样本中最喜欢B项目的人数百分比和其所在扇形图中的圆心角的度数;
(2)请把条形统计图补充完整;
(3)已知该校有1000人,请根据样本估计全校最喜欢足球的人数是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AE平分∠BAD交BC于E,∠CAE=15°,则下列结论:① △ODC是等边三角形;②BC=2AB;③∠AOE=135°; ④S△AOE=S△COE,其中正确的结论的个数有

A.1 B.2 C.3 D.4
相关试题

