搜索
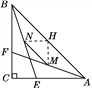
【题目】如图，在△ABC中，∠C＝90°，CA＝CB，E，F分别为CA，CB上一点，CE＝CF，M，N分别为AF，BE的中点，求证：AE＝
MN.
参考答案：
【答案】证明见解析.
【解析】试题分析：取AB的中点H，连接MH、NH，根据三角形的中位线平行于第三边并且等于第三边的一半可得NH=
AE，NH∥AE，MH=
BF，MH∥BF，再求出AE=BF，∠MHN=90°，判断出△MNG是等腰直角三角形，根据等腰直角三角形的性质可得NH=
MN，再表示出AE即可得证．
试题解析：如图，取AB的中点H，连接MH，NH，则MH＝
BF，
NH＝
AE.
∵CE＝CF，CA＝CB，∴AE＝BF.∴MH＝NH.
∵点M，N，N分别为AF，AB，BE的中点，
∴MH∥BF，NH∥AE.
∴∠AHM＝∠ABC，∠BHN＝∠BAC.
∴∠MHN＝180°－(∠AHM＋∠BHN)＝180°－(∠ABC＋∠BAC)＝90°.∴NH＝
MN.
∴AE＝2NH＝2×
MN＝
MN.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在反比例函数
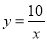（x＞0）的图象上，有一系列点A1、A2、A3、…、An、An+1，若A1的横坐标为2，且以后每点的横坐标与它前一个点的横坐标的差都为2．现分别过点A1、A2、A3、…、An、An+1作x轴与y轴的垂线段，构成若干个矩形如图所示，将图中阴影部分的面积从左到右依次记为S1，S2，S3，…，Sn，则S1= ，S1+S2+S3+…+Sn= ．（用n的代数式表示）．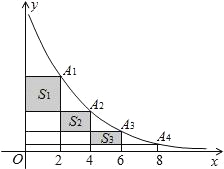
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果一个三角形的一个外角等于与它相邻的内角，这个三角形是（ ）
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
-
科目： 来源： 题型：
查看答案和解析>>【题目】多项式3x3﹣2x2﹣15的次数为（ ）
A.2
B.3
C.4
D.5 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，一副直角三角板满足AB=BC，AC=DE，∠ABC=∠DEF=90°，∠EDF=30°，
【操作1】将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上，再将三角板DEF绕点E旋转，并使边DE与边AB交于点P，边EF与边BC于点Q．
在旋转过程中，如图2，当
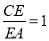时，EP与EQ满足怎样的数量关系？并给出证明．【操作2】在旋转过程中，如图3，当
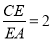时EP与EQ满足怎样的数量关系？，并说明理由．【总结操作】根据你以上的探究结果，试写出
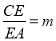当时，EP与EQ满足的数量关系是什么？其中m的取值范围是什么？（直接写出结论，不必证明）．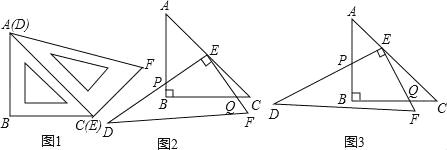
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB∥CD，OE平分∠BOC，OF⊥OE，OP⊥CD，∠ABO=a°．则下列结论：①∠BOE=
（180﹣a）°；②OF平分∠BOD；③∠POE=∠BOF；④∠POB=2∠DOF．其中正确结论（填编号）．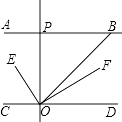 
-
科目： 来源： 题型：
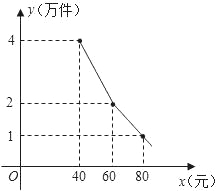
查看答案和解析>>【题目】为了扶持大学生自主创业，市政府提供了80万元无息贷款，用于某大学生开办公司生产并销售自主研发的一种电子产品，并约定用该公司经营的利润逐步偿还无息贷款．已知该产品的生产成本为每件40元，员工每人每月的工资为2500元，公司每月需支付其它费用15万元．该产品每月销售量y（万件）与销售单价x（元）之间的函数关系如图所示．
（1）求月销售量y（万件）与销售单价x（元）之间的函数关系式；
（2）当销售单价定为50元时，为保证公司月利润达到5万元（利润=销售额﹣生产成本﹣员工工资﹣其它费用），该公司可安排员工多少人？
（3）若该公司有80名员工，则该公司最早可在几个月后还清无息贷款？
相关试题
