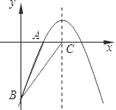
【题目】如图,已知二次函数y=﹣![]() +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.
(1)求这个二次函数的解析式;
(2)求当x满足什么条件时,函数值大于0?;
(3)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.
参考答案:
【答案】(1)y=﹣![]() +4x﹣6;(2)2<x<6;(3)S△ABC=6.
+4x﹣6;(2)2<x<6;(3)S△ABC=6.
【解析】试题分析:
(1)把A、B的坐标代入![]() 列方程组解得b、c的值即可得到二次函数的解析式;
列方程组解得b、c的值即可得到二次函数的解析式;
(2)由(1)中所求解析式,求得二次函数与x轴的交点坐标,结合图象即可求得当y>0时,x的取值范围;
(3)先由(1)中所求解析式求得点C的坐标,结合已知的点A、B的坐标即可求得△ABC的面积.
试题解析:
(1)把A(2,0)、B(0,﹣6)代入![]() ,
,
得: ![]() ,解得:
,解得: ![]() ,
,
∴这个二次函数的解析式为: ![]() .
.
(2)当![]() 时,可得:
时,可得: ![]() ,解得:
,解得: ![]() ,
,
∴图象与x轴交于两点,坐标分别为(2,0)和(6,0)
结合图象可知,当2<x<6时,
二次函数![]() 的函数值大于0.
的函数值大于0.
(3)∵二次函数![]() ,
,
∴该抛物线对称轴为直线![]() ,
,
∴点C的坐标为(4,0),
∴AC=OC﹣OA=4﹣2=2,
∴S△ABC=![]() AC×OB=
AC×OB=![]() ×2×6=6.
×2×6=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

-
科目: 来源: 题型:
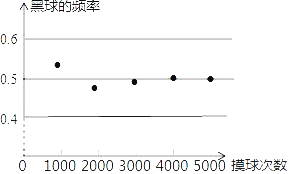
查看答案和解析>>【题目】一个不透明的袋子里装有黑白两种颜色的球其40只,这些球除颜色外都相同.小明从袋子中随机摸一个球,记下颜色后放回,不断重复,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
(1)摸到黑球的频率会接近 (精确到0.1);
(2)估计袋中黑球的个数为 只:
(3)若小明又将一些相同的黑球放进了这个不透明的袋子里,然后再次进行摸球试验,当重复大量试验后,发现黑球的频率稳定在0.6左右,则小明后来放进了 个黑球.
-
科目: 来源: 题型:
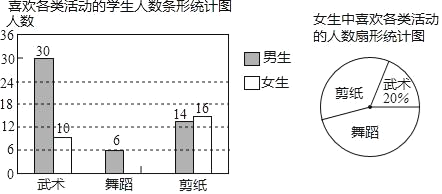
查看答案和解析>>【题目】某校开设武术、舞蹈、剪纸三项活动课程,为了了解学生对这三项活动课程的兴趣情况,随机抽取了部分学生进行调查(每人从中只能选一顶),并将调查结果绘制成下面两幅统计图,请你结合图中信息解答问题.
(1)将条形统计图补充完整;
(2)本次抽样调查的样本容量是 ;
(3)在扇形统计图中,计算女生喜欢剪纸活动课程人数对应的圆心角度数;
(4)已知该校有1200名学生,请结合数据简要分析该校学生对三项活动课程的兴趣情况.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,隧道的截面由抛物线ADC和矩形AOBC构成,矩形的长OB是12m,宽OA是4m.拱顶D到地面OB的距离是10m.若以O原点,OB所在的直线为x轴,OA所在的直线为y轴,建立直角坐标系.
(1)画出直角坐标系xOy,并求出抛物线ADC的函数表达式;
(2)在抛物线型拱壁E、F处安装两盏灯,它们离地面OB的高度都是8m,则这两盏灯的水平距离EF是多少米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是等边△ABC的外心,BO的延长线和⊙O相交于点D,连接DC,DA,OA,OC.
(1)求证:△BOC≌△CDA;
(2)若AB=
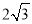 ,求阴影部分的面积.
,求阴影部分的面积.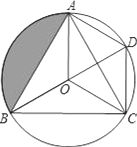
-
科目: 来源: 题型:
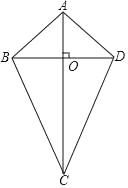
查看答案和解析>>【题目】定义:一条对角线垂直平分另一条对角线的四边形叫做筝形,如图,筝形ABCD的对角线AC、BD相交于点O.且AC垂直平分BD.
(1)请结合图形,写出筝形两种不同类型的性质:性质1: ;性质2: .
(2)若AB∥CD,求证:四边形ABCD为菱形.
相关试题

