Question

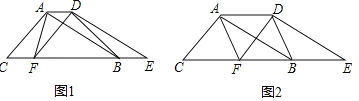
【题目】如图，两个全等的△ABC和△DEF重叠在一起，固定△ABC，将△DEF进行如下变换：

（1）如图1，△DEF沿直线CB向右平移（即点F在线段CB上移动），连接AF、AD、BD，请直接写出S△ABC与S四边形AFBD的关系

（2）如图2，当点F平移到线段BC的中点时，若四边形AFBD为正方形，那么△ABC应满足什么条件：请给出证明；

（3）在（2）的条件下，将△DEF沿DF折叠，点E落在FA的延长线上的点G处，连接CG，请你画出图形，此时CG与CF有何数量关系．

Answer 1

【答案】（1）S△ABC=S四边形AFBD；（2）四边形AFBD为正方形；（3）CG=CF．

【解析】

试题分析：（1）利用平行线的性质以及三角形面积关系，得出答案；

（2）利用平行四边形的判定得出四边形AFBD为平行四边形，进而得出AF=BC=BF，求出答案；

（3）根据题意画出图形，设CF=k，利用勾股定理求出即可．

解：（1）S△ABC=S四边形AFBD，

理由：由题意可得：AD∥EC，

则S△ADF=S△ABD，

故S△ACF=S△ADF=S△ABD，

则S△ABC=S四边形AFBD；

（2）△ABC为等腰直角三角形，即：AB=AC，∠BAC=90°，

理由如下：

∵F为BC的中点，

∴CF=BF，

∵CF=AD，

∴AD=BF，

又∵AD∥BF，

∴四边形AFBD为平行四边形，

∵AB=AC，F为BC的中点，

∴AF⊥BC，

∴平行四边形AFBD为矩形

∵∠BAC=90°，F为BC的中点，

∴AF=BC=BF，

∴四边形AFBD为正方形；

（3）如图3所示：

由（2）知，△ABC为等腰直角三角形，AF⊥BC，

设CF=k，则GF=EF=CB=2k，

由勾股定理得：CG=k，

∴CG=CF．