【题目】计算
(1)-5+2-13+4
(2)(-2)×(-8)-9÷(-3)
(3)(-18)×(-![]() )
)
(4)-(-3![]() )+12.5+(-16
)+12.5+(-16![]() )+(-2.5)
)+(-2.5)
参考答案:
【答案】(1)-12;(2)19;(3)-7;(4)-3![]()
【解析】
(1)从左向右依次计算即可.
(2)首先计算乘除法,然后计算减法即可.
(3)应用乘法分配律计算即可.
(4)应用加法交换律和加法结合律,求出算式的值是多少即可.
(1)-5+2-13+4
=-3-13+4
=-12
(2)(-2)×(-8)-9÷(-3)
=16+3
=19
(3)(-18)×(-![]() )
)
=(-18)×(-![]() )+(-18)×
)+(-18)×![]() +(-18)×(-
+(-18)×(-![]() )
)
=2-12+3
=-7
(4)-(-3![]() )+12.5+(-16
)+12.5+(-16![]() )+(-2.5)
)+(-2.5)
=[-(-3![]() )+(-16
)+(-16![]() )]+[12.5+(-2.5)]
)]+[12.5+(-2.5)]
=(-13![]() )+10
)+10
=-3![]()
-
科目: 来源: 题型:
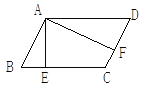
查看答案和解析>>【题目】如图,已知□ABCD中,AE⊥BC,AF⊥DC,BC∶CD= 3∶2,AB=EC,则∠EAF=( )
A.
 B.
B. 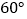 C.
C. 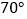 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】现在电器进入销售旺季,福清某电器超市销售每台进价分别为
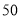 元、
元、 元的
元的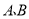 两种型号的电器,下表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入-进货成本)
两种型号的电器,下表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入-进货成本)销售时段
销售数量
销售收入
 种型号
种型号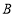 种型号
种型号第一周
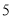 台
台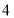 台
台 元
元第二周
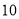 台
台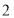 台
台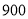 元
元(1)求
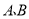 两种型号的电器销售单价;
两种型号的电器销售单价;(2)若超市准备用不超过
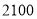 元的金额再采购这种型号的电器共
元的金额再采购这种型号的电器共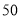 台,销售完这
台,销售完这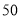 台电器实现利润超过
台电器实现利润超过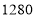 元的目标,请给出相应的采购方案;并求出利润的最大值.
元的目标,请给出相应的采购方案;并求出利润的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】乘法公式的探究与应用:

(1)如图甲,边长为a的大正方形中有一个边长为b的小正方形,请你写出阴影部分面积是 (写成两数平方差的形式)
(2)小颖将阴影部分裁下来,重新拼成一个长方形,如图乙,则长方形的长是 ,宽是 ,面积是 (写成多项式乘法的形式).
(3)比较甲乙两图阴影部分的面积,可以得到公式 (用式子表达)
(4)运用你所得到的公式计算:10.3×9.7.
-
科目: 来源: 题型:
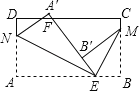
查看答案和解析>>【题目】如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF,将∠BEF对折,点B落在直线EF上的点B'处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A'处,得折痕EN,若∠DNA'的度数为α,请用含α的式子表示∠BME的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=x2+mx+1,当0<x≤2时的函数值总是非负数,则实数m的取值范围为( )
A. m≥﹣2 B. ﹣4≤m≤﹣2 C. m≥﹣4 D. m≤﹣4或m≥﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=5,AD、AB、BC分别与⊙O相切于E、F、G三点,过点D作⊙O的切线交BC于点M,则DM的长为( )

A.
 B.
B.  C.
C.  D.
D. 
相关试题

