【题目】如图,已知一个由小正方体组成的几何体的左视图和俯视图.

![]() 该几何体最少需要几块小正方体?最多可以有几块小正方体?
该几何体最少需要几块小正方体?最多可以有几块小正方体?
![]() 请画出该几何体的所有可能的主视图.
请画出该几何体的所有可能的主视图.
参考答案:
【答案】(1)该几何体最少需要![]() 块小正方体;最多需要
块小正方体;最多需要![]() 块小正方体.(2)详见解析.
块小正方体.(2)详见解析.
【解析】
(1)由俯视图可得最底层的几何体的个数,由左视图第二层正方形的个数可得第二层最少需要几块正方体,相加即可得到该几何体最少需要几块小正方体;由俯视图和左视图可得第二层最多需要几块小正方体,再加上最底层的正方体的个数即可得到最多可以有几块小正方体.
(2)根据俯视图可知有三列,由左视图即可得出所有的组成图形,即可得出主视图.
解:俯视图中有![]() 个正方形,那么组合几何体的最底层有
个正方形,那么组合几何体的最底层有![]() 个正方体,
个正方体,![]() 由左视图第二层有
由左视图第二层有![]() 个正方形可得组合几何体的第二层最少有
个正方形可得组合几何体的第二层最少有![]() 个正方体,俯视图从上边数第一行的第二层最多可有
个正方体,俯视图从上边数第一行的第二层最多可有![]() 个正方体,所以该几何体最少需要
个正方体,所以该几何体最少需要![]() 块小正方体;最多需要
块小正方体;最多需要![]() 块小正方体.
块小正方体.
![]() 作图如下:
作图如下:
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于受到手机更新换代的影响,某手机店经销
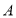 型号手机四月售价比三月每台降价500元.如果卖出相同数量的
型号手机四月售价比三月每台降价500元.如果卖出相同数量的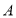 型号手机,那么三月销售额为9万元,四月销售额只有8万元.
型号手机,那么三月销售额为9万元,四月销售额只有8万元.(1)三月
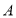 型号手机每台售价为多少元?
型号手机每台售价为多少元?(2)为了提高利润,该店计划五月购进
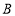 型号手机销售,已知
型号手机销售,已知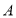 型号每台进价为3500元,
型号每台进价为3500元,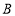 型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?
型号每台进价为4000元,预计用不多于7.6万元且不少于7.4万元的资金购进这两种手机共20台,请问有几种进货方案?(3)该店计划六月对
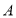 型号的尾货进行销售,决定在四月售价基础上每售出一台
型号的尾货进行销售,决定在四月售价基础上每售出一台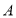 型号手机再返还顾客现金
型号手机再返还顾客现金 元,而
元,而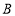 型号按销售价4400元销售,如要使(2)中所有方案获利相同,
型号按销售价4400元销售,如要使(2)中所有方案获利相同,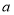 应取何值?
应取何值? -
科目: 来源: 题型:
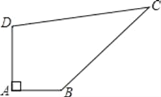
查看答案和解析>>【题目】已知某开发区有一块四边形的空地ABCD,如图所示,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
-
科目: 来源: 题型:
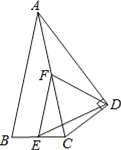
查看答案和解析>>【题目】如图,△ABC中,AB=AC,E、F分别是BC、AC的中点,以AC为斜边作Rt△ADC.
(1)求证:FE=FD;
(2)若∠CAD=∠CAB=24°,求∠EDF的度数
-
科目: 来源: 题型:
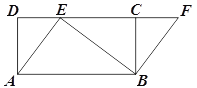
查看答案和解析>>【题目】如图,四边形ABCD是矩形,点E在CD边上,点F在DC延长线上,AE=BF.
(1)求证:四边形ABFE是平行四边形;
(2)若∠BEF=∠DAE,AE=3,BE=4,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
【1】如图1,损矩形ABCD,∠ABC=∠ADC=90°,则该损矩形的直径是线段 .
【1】在线段AC上确定一点P,使损矩形的四个顶点都在以P为圆心的同一圆上(即损矩形的四个顶点在同一个圆上),请作出这个圆,并说明你的理由. 友情提醒:“尺规作图”不要求写作法,但要保留作图痕迹.
【1】如图2,△ABC中,∠ABC=90°,以AC为一边向形外作菱形ACEF,D为菱形ACEF的中心,连结BD,当BD平分∠ABC时,判断四边形ACEF为何种特殊的四边形?请说明理由. 若此时AB=3,BD=
 ,求BC的长.
,求BC的长.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知圆内接四边形ABCD的对角线AC、BD交于点N,点M在对角线BD上,且满足∠BAM=∠DAN,∠BCM=∠DCN.
求证:(1)M为BD的中点;(2)
 .
.
相关试题

