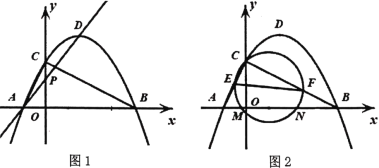
【题目】如图，二次函数（、为参数，其中）的图象与轴交于、两点，与轴交于点，顶点为．

（1）若，求的值（结果用含的式子表示）；

（2）若是等腰三角形，直线与轴交于点，且．求抛物线的解析式；

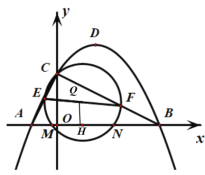
（3）如图，已知，、分别是和上的动点，且，若以为直径的圆经过点，并交轴于、两点，求的最大值．

【答案】（1）tan∠CBA=－2a；（2）；（3）MN的最大值=

【解析】

（1）将代入函数解析式，求得B点坐标，在直角三角形BOC中，利用正切定义直接求得；

（2）利用对称轴可知D的横坐标，过D做DH⊥x轴，交x轴于点H，因为OP∥DH，利用平行线分线段成比例，求得A、B两点坐标，代入解析式可得到，再对分情况讨论即可；

（3）利用圆周角定理可知解得a，求得C点，同时由已知EF=3，可知取EF的中点Q，过Q做QH⊥X轴于点H，则Q在以C为圆心，为半径的圆上运动，在Rt△QHN中，，求HN的最大值等价求QH的最小值，求得QH推得HN，进而得到MN.

（1）∵

∴

∴A（-2，0），B（5，0），C（-10a，0）

∴tan∠CBA=

（2）由已知

过D做DH⊥X轴，交X轴于点H

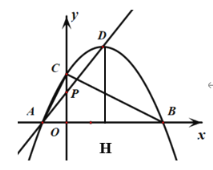
∵OP∥DH，AP：DP=2：3，

∴

∴OA=1，A（－1，0），B（4，0）

∴

∴

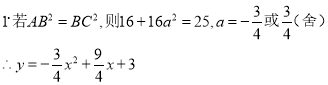
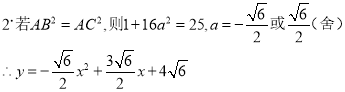
（3）∵A（－1，0），B（4，0）且以EF为直径的圆经过点C

∴，解得

∴C（0.2）

∵

取EF的中点Q，过Q做QH⊥x轴于点H，则Q在以C为圆心，为半径的圆上运动

∵MN=2HN

在Rt△QHN中，，求HN的最大值等价求QH的最小值

∵QH的最小值=

∴HN的最大值=

∴MN的最大值=

关闭