【题目】已知,如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P,
求证:BP=2PQ.
参考答案:
【答案】证明:∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,  ,
,
∴△ABE≌△CAD(SAS),
∴∠1=∠2,
∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,
∵BQ⊥AD,
∴∠PBQ=90°﹣∠BPQ=90°﹣60°=30°,
∴BP=2PQ.
【解析】根据等边三角形的性质可得AB=AC,∠BAE=∠C=60°,再利用“边角边”证明△ABE和△CAD全等,根据全等三角形对应角相等可得∠1=∠2,然后求出∠BPQ=60°,再根据直角三角形两锐角互余求出∠PBQ=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半证明即可.
-
科目: 来源: 题型:
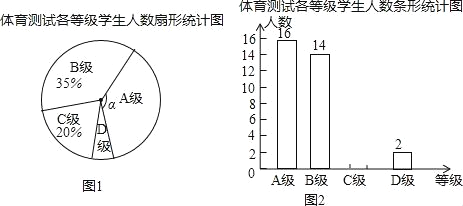
查看答案和解析>>【题目】为了解某区九年级学生身体素质情况,该区从全区九年级学生中随机抽取了部分学生进行了一次体育考试科目测试(把测试结果分为四个等级:A级:优秀:B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如图两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ;
(2)求图1中∠α的度数是 °,把图2条形统计图补充完整;
(3)该区九年级有学生3500名,如果全部参加这次体育科目测试,请估计不及格的人数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,△ABC中AC边上的高是( )

A.线段BE
B.线段CH
C.线段AD
D.线段BG -
科目: 来源: 题型:
查看答案和解析>>【题目】25°的角的余角的度数与它的补角的度数的比是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( )

A.40°
B.30°
C.20°
D.10° -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x 2 +3=2x的根的情况为( )
A. 没有实数根
B. 有两个相等的实数根
C. 有一个实数根
D. 有两个不相等的实数根
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+1(a<0)的图象过点(1,0)和(x1,0),且﹣2<x1<1,下列5个判断中:①b<0;②b﹣a<0;③a>b﹣1;④a<﹣
 ;⑤2a<b+
;⑤2a<b+ ,正确的是( )
,正确的是( )A. ①③ B. ①②③ C. ①②③⑤ D. ①③④⑤
相关试题

