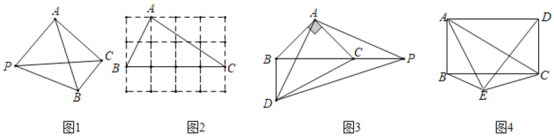
【题目】如图1，平面内有一点到的三个顶点的距离分别为若有，则称点为关于点的勾股点．

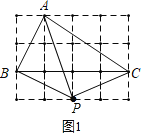
如图2，在的方格纸中，每个小正方形的边长均为的顶点在格点上，请找出所有的格点，使点为关于点的勾股点；

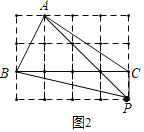
如图3， 为等腰直角三角形，是斜边延长线上一点，连接，以为直角边作等腰直角三角形 (点顺时针排列)，，连接 求证：点为关于点的勾股点；

如图4，点是矩形外一点，且点是关于点的勾股点，若，求的长．

【答案】见解析；见解析；

【解析】

（1）如图1，图2，求出PA2，PB2，PC2，得到PC2+PB2=PA2，即得出点P是△ABC关于点A的勾股点；

（2）证明△ABD≌△ACP（SAS），得出BD=CP，∠ABD=∠ACP=135°，证明∠DBP=90°，则结论得证；

（3）由条件“点C是△ABE关于点A的勾股点”可得CE=CD=5，如图3，过点E作MN⊥AB于点M，交DC的延长线于点N，设AM=DN=x，则CN=DN-CD=x-5，由勾股定理可得62-x2=52-（x-5）2，解得：x=，则求出AM，ME的长，则答案可得出．

（1）如图1，

∵PA2=12+32=10，PB2=12+22=5，PC2=PB2=5，

∴PA2=PC2+PB2，

∴点P是△ABC关于点A的勾股点；

如图2，

∵PA2=32+32=18，PB2=12+42=17，PC2=1，

∴PA2=PC2+PB2，

∴点P是△ABC关于点A的勾股点；

（2）∵△ABC和△APD为等腰直角三角形，

∴AB=AC，AD=AP，∠BAC=∠DAP=90°，

∴∠BAC-∠DAC=∠DAP-∠DAC，

即∠BAD=∠CAP，

∴△ABD≌△ACP（SAS），

∴BD=PC，∠ABD=∠ACP=135°，

∵∠ABC=45°，

∴∠DBP=∠ABD-∠ABC=135°-45°=90°，

∴BD2+PB2=PD2，

∴PC2+PB2=PD2，

∴点P为△BDC关于点D的勾股点．

（3）解：∵矩形ABCD中，AD=8，

∴AD=BC=8，CD=AB，

∵AD=DE，

∴DE=8，

∵点C是△ABE关于点A的勾股点，

∴AC2=CB2+CE2，

∵AC2=AB2+BC2，

∴CE=CD=5，

如图3，过点E作MN⊥AB于点M，交DC的延长线于点N，

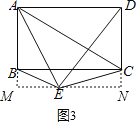
∴∠AME=∠MND=90°，

∴四边形AMND是矩形，

∴MN=AD=8，AM=DN，

设AM=DN=x，则CN=DN-CD=x-5，

∵Rt△DEN中，EN2+DN2=DE2；Rt△CEN中，EN2+CN2=CE2，

∴DE2-DN2=CE2-CN2，

∴62-x2=52-（x-5）2

解得：x=，

∴，，

∴，

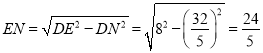∴Rt△AME中，．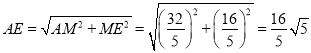

关闭