【题目】白色污染(White Pollution)是人们对难降解的塑料垃圾(多指塑料袋)污染环境现象的一种形象称谓.为了让全校同学感受丢弃塑料袋对环境的影响,小彬随机抽取某小区![]() 户居民,记录了这些家庭
户居民,记录了这些家庭![]() 年某个月丢弃塑料袋的数量(单位:个):
年某个月丢弃塑料袋的数量(单位:个):
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
请根据上述数据,解答以下问题:
(1)小彬按“组距为![]() ”列出了如下的频数分布表(每组数据含最小值),请将表中空缺的部分补充完整,并补全频数直方图;
”列出了如下的频数分布表(每组数据含最小值),请将表中空缺的部分补充完整,并补全频数直方图;
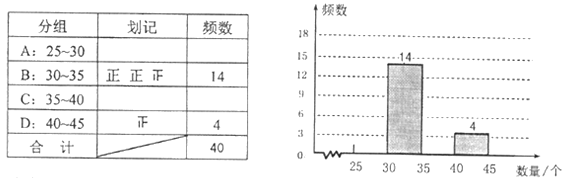
(2)根据(1)中的直方图可以看出,这![]() 户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
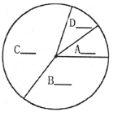
(3)根据频数分布表,小彬又画出了右图所示的扇形统计图.请将统计图中各组占总数的百分比填在图中,并求出![]() 组对应的扇形圆心角的度数;
组对应的扇形圆心角的度数;
(4)若小区共有![]() 户居民家庭,请你估计每月丢弃的塑料袋数量不小于
户居民家庭,请你估计每月丢弃的塑料袋数量不小于![]() 个家庭个数.
个家庭个数.
参考答案:
【答案】(1)见解析(2)C(3)162°(4)900个
【解析】
(1)根据数据即可补全表格与直方图;(2)由图可知C组的家庭最多;(3)
分别算出各组的占比,再用C组占比乘以360°即可求出圆心角度数;(4)先求出不小于![]() 个家庭的占比,再乘以1000即可.
个家庭的占比,再乘以1000即可.
(1)补全表格与直方图如下图:
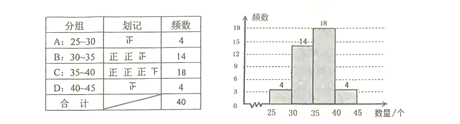
(2)由直方图可知这个月丢弃塑料袋的个数在C组的家庭最多;
(3)A组占比为:![]() ,
,
B组占比为:![]() ,
,
C组占比为:![]() ,圆心角度数为360°×45%=162°,
,圆心角度数为360°×45%=162°,
A组占比为:![]() ,
,
补全扇形统计图为
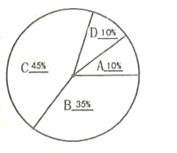
(4)不小于![]() 个家庭的占比为35%+45%+10%=90%,
个家庭的占比为35%+45%+10%=90%,
故小区每月丢弃的塑料袋数量不小于![]() 个家庭个数为1000×90%=900个.
个家庭个数为1000×90%=900个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在△ABC中,∠A=30°,∠C=105°,AC=2
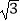 ,求AB的长.
,求AB的长.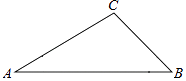
-
科目: 来源: 题型:
查看答案和解析>>【题目】李明上星期买进某公司股票7000股,每股27元,下表为本周每日该股票的涨跌情况
 单位:元
单位:元
星期
一
二
三
四
五
六
每股涨跌






 这六天中,哪几天的股票是上涨的?哪几天的股票是下跌的?
这六天中,哪几天的股票是上涨的?哪几天的股票是下跌的? 哪天股票上涨的最多?你能算出这天收盘时每股是多少元吗?
哪天股票上涨的最多?你能算出这天收盘时每股是多少元吗? 本周六收盘时每股是多少元?
本周六收盘时每股是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
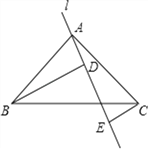
查看答案和解析>>【题目】如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l于D,CE⊥AE,若BD>CE,试问:
(1)AD与CE的大小关系如何?请说明理由;
(2)线段BD,DE,CE之间的数量之间关系如何?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MAN=120°,AC平分∠MAN.B、D分别在射线AN、AM上.
(1)在图1中,当∠ABC=∠ADC=90°时,求证:AD+AB=AC
(2)若把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,如图2所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

(图1) (图2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
相关试题

