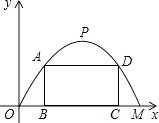
【题目】施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米,现在O点为原点,OM所在直线为x轴建立直角坐标系(如图所示). 
(1)直接写出点M及抛物线顶点P的坐标;
(2)求出这条抛物线的函数解析式;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABCD,使A,D点在抛物线上,B,C点在地面OM上.为了筹备材料,需求出“脚手架”三根木杆AB,AD,DC的长度之和的最大值是多少?请你帮施工队计算一下.
参考答案:
【答案】
(1)解:M(12,0),P(6,6)
(2)解:∵顶点坐标(6,6)
∴设y=a(x﹣6)2+6(a≠0)
又∵图象经过(0,0)
∴0=a(0﹣6)2+6
∴ ![]()
∴这条抛物线的函数解析式为y=﹣ ![]() (x﹣6)2+6,即y=﹣
(x﹣6)2+6,即y=﹣ ![]() x2+2x
x2+2x
(3)解:设A(x,y)
∴A(x,﹣ ![]() (x﹣6)2+6)
(x﹣6)2+6)
∵四边形ABCD是矩形,
∴AB=DC=﹣ ![]() (x﹣6)2+6,
(x﹣6)2+6,
根据抛物线的轴对称性,可得:OB=CM=x,
∴BC=12﹣2x,即AD=12﹣2x,
∴令L=AB+AD+DC=2[﹣ ![]() (x﹣6)2+6]+12﹣2x=﹣
(x﹣6)2+6]+12﹣2x=﹣ ![]() x2+2x+12=﹣
x2+2x+12=﹣ ![]() (x﹣3)2+15.
(x﹣3)2+15.
∴当x=3,L最大值为15
∴AB、AD、DC的长度之和最大值为15米.
【解析】确定了抛物线的顶点式,可以设抛物线的顶点式,又过原点(0,0),就可以确定抛物线解析式;设OB=x,由对称性得CM=x,这样就可以用含x的式子表示AB、AD、CD了,为求三根木杆AB、AD、DC的长度之和的最大值,提供依据.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进一批单价为16元的日用品,销售一段时间后,为了获得更多利润,商店决定提高销售价格.经试验发现,若按每件20元的价格销售时,每月能卖360件;若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其它因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少(总利润=总收入﹣总成本)? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=
 ,BG=
,BG= ,且
,且 、
、 满足下列关系:
满足下列关系: ,
, ,则GH= .
,则GH= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长是a,宽是b的长方形硬纸板的四周各剪去一个边长为c的正方形(a>b>2c).再折合成一个无盖的长方体盒子(纸板的厚度忽略不计).
(1)若a=12,b=7,c=2,求折合成的长方体盒子的侧面积是多少?
(2)请用含a,b,c的代数式表示折成的长方体盒子的底面周长;
(3)如果把长方体硬纸板的四周剪去2个边长为c的正方形和2个同样形状、同样大小的长方形,然后折合成一个有盖的长方体盒子,那么它的底面周长是多少?(用含a,b,c的代数式表示)

-
科目: 来源: 题型:
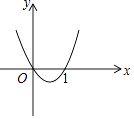
查看答案和解析>>【题目】如图为二次函数y=ax2+bx+c的图象,下列各式中:①a>0,②b>0,③c=0,④c=1,⑤a+b+c=0.正确的只有( )
A.①④
B.②③④
C.③④⑤
D.①③⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知点A(3,4),将OA绕坐标原点O逆时针旋转90°至OA′,则点A′的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.

(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
相关试题

