【题目】如图,在Rt△ABC中,∠C=90°,点D在AB上,以AD为直径的⊙O与BC相
交于点E,且AE平分∠BAC.
(1)求证:BC是⊙O的切线;
(2)若∠EAB=30°,OD=3,求图中阴影部分的面积.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析: ![]() 连接
连接![]() 证明
证明![]() ,从而得出∠OEB=∠C=90°,从而得证.
,从而得出∠OEB=∠C=90°,从而得证.
![]() 阴影部分的面积等于三角形的面积减去扇形的面积.
阴影部分的面积等于三角形的面积减去扇形的面积.
试题解析: ![]() 连接
连接![]()
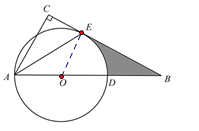
∵AE平分∠BAC,
∴∠CAE=∠EAD,
∵OA=OE,
∴∠EAD=∠OEA,
∴∠OEA=∠CAE,
![]() ,
,
∴∠OEB=∠C=90°,
∴OE⊥BC,且点E在⊙O上,
∴BC是⊙O的切线.
(2)解: ∵∠EAB=30°,
∴∠EOD=60°,
∵∠OEB=90°,
∴∠B=30°,
∴OB=2OE=2OD=6,
∴![]()
![]() 扇形
扇形![]() 的面积
的面积![]()
阴影部分的面积为: ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列调查中,适合采用全面调查方式的是( )
A. 了解某班同学某次体育模拟考的测试成绩
B. 调查福州闯江的水质情况
C. 调查“中国诗词大会”的收视率
D. 调查某批次汽车的抗撞击能力
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知xy=2,x+y=3,则x2y+xy2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有房间40间,当每间房间定价为300元/天时,可全部住满.每间房间定价每增加10元/天,未入住的房间将增加1间.入住的房间的维护费为20元/天,未入住的房间的维护费为5元/天.
(1)当每间房间定价为360元/天时,入住的房间有多少间?
(2)设该宾馆未入住的房间有x间,
①用x的代数式表示每间房间的定价;
②当每间房间定价为多少元/天时,该宾馆每天的收入可达到11 350元?(宾馆每天的收入=入住的房费-维护费)
-
科目: 来源: 题型:
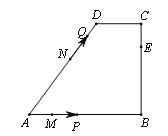
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M、N、E分别是AB、AD、CB上的点,AM=CE=1,AN=3,点P从点M出发,以每秒1个单位长度的速度沿折线MB-BE向点E运动,同时点Q从点N,以相同的速度沿折线ND-DC-CE向点E运动,设△APQ的面积为S,运动的时间为t秒,则S与t函数关系的大致图象为( )
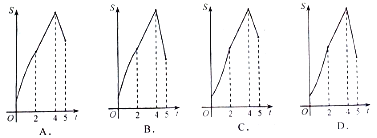
A. A B. B C. C D. D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,P1、P2是反比例函数y=
 (k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(k>0)在第一象限图象上的两点,点A1的坐标为(4,0).若△P1OA1与△P2A1A2均为等腰直角三角形,其中点P1、P2为直角顶点.
(1)直接写出反比例函数的解析式.
(2)①求P2的坐标.②根据图象直接写出在第一象限内,当x满足什么条件时,经过点P1、P2的一次函数的函数值大于反比例函数y=
 的函数值.
的函数值.
相关试题

