【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.

参考答案:
【答案】(1)、证明过程见解析;(2)、∠QMC=60°;(3)、∠QMC=120°.
【解析】
试题分析:(1)、根据等边三角形可得∠ABQ=∠CAP,AB=CA,根据速度相同可得AP=BQ,从而得出三角形全等;(2)、根据△ABQ≌△CAP得出∠BAQ=∠ACP,然后根据∠QMC=∠BAQ+∠MACC=∠BAC得出答案;(3)、根据△ABQ≌△CAP得出∠BAQ=∠ACP,然后根据∠QMC=∠ACP+∠APM=180°-∠PAC得出答案.
试题解析:(1)、∵△ABC是等边三角形 ∴∠ABQ=∠CAP,AB=CA, 又∵点P、Q运动速度相同,
∴AP=BQ, 在△ABQ与△CAP中,AB=AC,∠ABQ=∠CAP,AP=BQ ∴△ABQ≌△CAP(SAS);
(2)、点P、Q在运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP, ∴∠BAQ=∠ACP, ∵∠QMC=∠ACP+∠MAC, ∴∠QMC=∠BAQ+∠MAC=∠BAC=60°
(3)、点P、Q在运动到终点后继续在射线AB、BC上运动时,∠QMC不变.
理由:∵△ABQ≌△CAP, ∴∠BAQ=∠ACP, ∵∠QMC=∠BAQ+∠APM,
∴∠QMC=∠ACP+∠APM=180°-∠PAC=180°-60°=120°
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O到
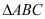 的两边AB、AC所在直线的距离相等,且OB=OC。
的两边AB、AC所在直线的距离相等,且OB=OC。(1)如图1,若点O在边BC上, 求证:AB=AC;(2)、如图2,若点O在
 的内部, 求证:AB=AC;
的内部, 求证:AB=AC;(3)若点O在
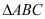 的外部,AB=AC成立吗?请画图表示。
的外部,AB=AC成立吗?请画图表示。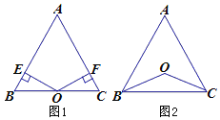
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分5分)画图并填空:
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.
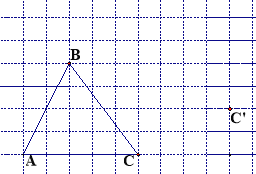
(1)画出平移后的△A′B′C′,(利用网格点和三角板画图)
(2)画出AB边上的高线CD;
(3)画出BC边上的中线AE;
(4)在平移过程中高CD扫过的面积为 .(网格中,每一小格单位长度为1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2+2x﹣5=0;
(2)x(x﹣8)=16
(3)(x﹣2)2﹣4=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形中有两边长分别为3和7,则这个三角的周长为
A. 13 B. 17 C. 10 或 13 D. 13 或 17
-
科目: 来源: 题型:
查看答案和解析>>【题目】将直线y=2x向上平移1个单位,得到的一次函数的解析式是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】据报道,春节期间微信红包收发高达3270000000次,数字3270000000用科学记数法表示为 _____
相关试题

