【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交弧AC于点D,过点D作⊙O的切线,交BA的延长线于点E. 
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=2时,求出四边形ACDE的面积. 
参考答案:
【答案】
(1)证明:∵F为弦AC(非直径)的中点,
∴AF=CF,
∴OD⊥AC,
∵DE切⊙O于点D,
∴OD⊥DE,
∴AC∥DE
(2)证明:∵AC∥DE,且OA=AE,
∴F为OD的中点,即OF=FD,又∵AF=CF,
∠AFO=∠CFD,
∴△AFO≌△CFD(SAS),
∴S△AFO=S△CFD,
∴S四边形ACDE=S△ODE
在Rt△ODE中,OD=OA=AE=2,
∴OE=4,
∴DE= ![]() =2
=2 ![]()
∴S四边形ACDE=S△ODE= ![]() ×OD×OE=
×OD×OE= ![]() ×2×2
×2×2 ![]() =2
=2 ![]() .
.
【解析】(1)欲证明AC∥DE,只要证明AC⊥OD,ED⊥OD即可.(2)由△AFO≌△CFD(SAS),推出S△AFO=S△CFD , 推出S四边形ACDE=S△ODE , 求出△ODE的面积即可.
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1 , l2 , 过点(1,0)作x轴的垂线交l1于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l1于点A3 , 过点A3作y轴的垂线交l2于点A4 , …依次进行下去,则点A2017的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,OA=3,OC=2,点F是AB上的一个动点(F不与A,B重合),过点F的反比例函数y=
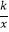 的图象与BC边交于点E.
的图象与BC边交于点E. 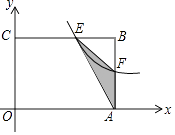
(1)当F为AB的中点时,求该函数的解析式;
(2)当k为何值时,△EFA的面积最大,最大面积是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下: 甲:79,86,82,85,83
乙:88,79,90,81,72.
回答下列问题:
(1)甲成绩的平均数是 , 乙成绩的平均数是;
(2)经计算知S甲2=6,S乙2=42.你认为选拔谁参加比赛更合适,说明理由;
(3)如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于80分的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+
 )海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
)海里的C处,为了防止某国海巡警干扰,就请求我A处的渔监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校是乒乓球体育传统项目学校,为进一步推动该项目的开展,学校准备到体育用品店购买直拍球拍和横拍球拍若干副,并且每买一副球拍必须要买10个乒乓球,乒乓球的单价为2元/个,若购买20副直拍球拍和15副横拍球拍花费9000元;购买10副横拍球拍比购买5副直拍球拍多花费1600元.
(1)求两种球拍每副各多少元?
(2)若学校购买两种球拍共40副,且直拍球拍的数量不多于横拍球拍数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
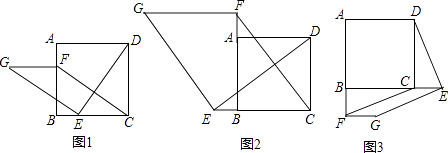
(1)请判断:FG与CE的数量关系是 , 位置关系是;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
相关试题

