【题目】计算:
①已知:a+![]() =1+
=1+![]() ,求a2+
,求a2+![]() 的值.
的值.
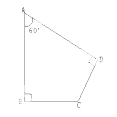
②如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AB=2,CD=1,求四边形ABCD的面积。
参考答案:
【答案】①![]() ;②
;②![]()
【解析】试题分析:①把 a+![]() =1+
=1+![]() 的两边分别平方,进一步整理得出a2+
的两边分别平方,进一步整理得出a2+![]() 的值.
的值.
②延长AD、BC交于E,根据直角三角形两锐角互余求出∠E=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半求出AE、CE,再利用勾股定理列式求出BE、DE,然后根据四边形的面积等于两个直角三角形的面积的差列式计算即可得解.
试题解析:
①∵a+![]() =1+
=1+![]() ,
,
∴(a+![]() )2=(1+
)2=(1+![]() )2,
)2,
∴a2+![]() +2=11+2
+2=11+2![]() ,
,
∴a2+![]() =9+2
=9+2![]() ;
;
②如图,延长AD、BC交于E.
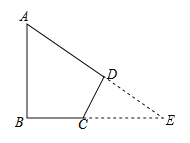
∵∠B=90°,∠A=60°,
∴∠E=90°-60°=30°,
在Rt△ABE和Rt△CDE中,∵AB=2,CD=1,
∴AE=2AB=2×4,CE=2CD=2×1=2,
由勾股定理得,BE=![]() ,
,
DE=![]() ,
,
∴S四边形ABCD=![]()
=![]()
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】刻画一组数据波动大小的统计量是( )
A. 平均数 B. 方差 C. 众数 D. 中位数
-
科目: 来源: 题型:
查看答案和解析>>【题目】比-1小2的数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】3.1415精确到百分位的近似数是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设
 ,
,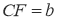 ,满足
,满足 .
.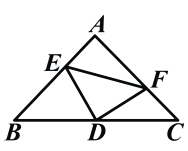
(1)求BE及CF的长。
(2)求证:
 。
。(3)在(1)的条件下,求△DEF的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a·a2=a3B.(-a2)2=-a4
C.3a+2a=5a2D.(a2b)3=a2·b3
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙三个不同品种的苹果树在同一地区进行对比试验,从每个品种的苹果树中随机各抽取10棵,对它们的产量进行统计,绘制统计表如下:
品种
甲
乙
丙
平均产量/(千克/棵)
90
90
方差
10.2
24.8
8.5
若从这三个品种中选择一个在该地区推广,则应选择的品种是( )
A.甲B.乙C.丙D.甲、乙中任选一个
相关试题

