【题目】如图,点P是矩形ABCD的边AD的一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是 . 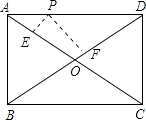
参考答案:
【答案】![]()
【解析】解:过P点作PE⊥AC,PF⊥BD, 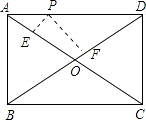
∵四边形ABCD是矩形,
∴AD⊥CD,
∴△PEA∽△CDA,
∴ ![]() ,
,
∵AC=BD= ![]() =5,
=5,
∴ ![]() …①,
…①,
同理:△PFD∽△BAD,
∴ ![]() ,
,
∴ ![]() …②,
…②,
∴①+②得: ![]() ,
,
∴PE+PF= ![]() ,
,
即点P到矩形的两条对角线AC和BD的距离之和是: ![]() .
.
故答案为: ![]() .
.
过P点作PE⊥AC,PF⊥BD,由矩形的性质可证△PEA∽△CDA和△PFD∽△BAD,根据 ![]() 和
和 ![]() ,即
,即 ![]() 和
和 ![]() ,两式相加得PE+PF=
,两式相加得PE+PF= ![]() ,即为点P到矩形的两条对角线AC和BD的距离之和.
,即为点P到矩形的两条对角线AC和BD的距离之和.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠MON=90°,线段AB长为6cm,AB两端分别在OM、ON上滑动,以AB为边作正方形ABCD,对角线AC、BD相交于点P,连结OC.
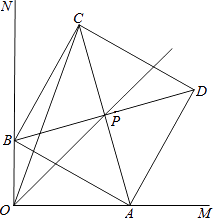
(1)求证:无论点A、点B怎样运动,点P都在∠AOB的平分线上;
(2)若OP=4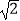 ,求OA的长.
,求OA的长.
(3)求OC的最大值(提示:取AB的中点Q,连接CQ、OQ,运用两点之间,线段最短) -
科目: 来源: 题型:
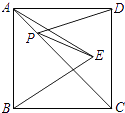
查看答案和解析>>【题目】如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A.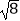
B.3
C.4
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某超市在“元旦”促销期间规定:超市内所有商品按标价的
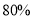 出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:
出售,同时当顾客在消费满一定金额后,按如下方案获得相应金额的奖券:消费金额
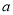 (元)的范围
(元)的范围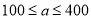
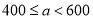
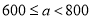
获得奖券金额(元)
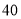
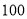
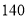
(符号
 表示
表示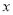 是大于或等于
是大于或等于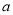 ,而小于
,而小于 的数)
的数)根据上述促销方法知道,顾客在超市内购物可以获得双重优惠,即顾客在超市内购物获得的优惠额
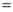 商品的折扣
商品的折扣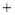 相应的奖券金额,例如:购买标价为
相应的奖券金额,例如:购买标价为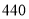 元的商品,则消费金额为:
元的商品,则消费金额为: 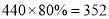 元,获得的优惠额为:
元,获得的优惠额为:  元.
元.(
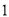 )购买一件标价为
)购买一件标价为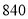 元的商品,求获得的优惠额.
元的商品,求获得的优惠额.(
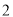 )对于标价在
)对于标价在 元与
元与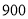 元之间(含
元之间(含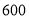 元和
元和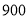 元)的商品,顾客购买标价为多少元的商品时可以得到
元)的商品,顾客购买标价为多少元的商品时可以得到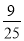 的优惠率.(设购买该商品得到的优惠率
的优惠率.(设购买该商品得到的优惠率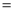 购买商品获得的优惠额
购买商品获得的优惠额 商品的标价)
商品的标价) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的一条边等于4,另一条边等于9,那么这个三角形的第三边是_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】八边形的内角和为_____;一个多边形的每个内角都是120°,则它是____边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=2,AC=
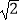 ,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为 .
,∠BAC=105°,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为 . 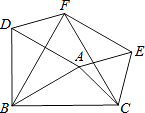
相关试题

