【题目】如图,小明所在教学楼的每层高度为3.5米,为了测量旗杆MN的高度,他在教学楼一楼的窗台A处测得旗杆顶部M的仰角为45°,他在二楼窗台B处测得M的仰角为31°,已知每层楼的窗台离该层的地面高度均为1米,求旗杆MN的高度;(结果保留两位小数)
(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)

参考答案:
【答案】旗杆MN的高度度约为9.75米.
【解析】
试题分析:过点M的水平线交直线AB于点H,设MH=x,则AH=x,结合等腰直角三角形的性质和解直角三角形ABH得到AB=AH﹣BH=x﹣0.60x=0.4x=3.5,由此求得MH的长度,则MN=AB+BH.
试题解析:过点M的水平线交直线AB于点H,
由题意,得∠AMH=∠MAH=45°,∠BMH=31°,AB=3.5,
设MH=x,则AH=x,BH=xtan31°=0.60x,
∴AB=AH﹣BH=x﹣0.60x=0.4x=3.5,
解得x=8.75,
则旗杆高度MN=x+1=9.75(米)
答:旗杆MN的高度度约为9.75米.

-
科目: 来源: 题型:
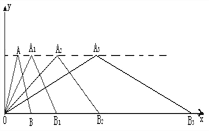
查看答案和解析>>【题目】如下图所示,在直角坐标系中,第一次将△OAB变换成△OA1B1,第二次将△OA1B1变换成△OA2B2,第三次将△OA2B2变换成△OA3B3, 已知A(1,3),A1 (2,3), A2 (4,3), A3 (8,3),B(2,0), B1 (4,0), B2 (8,0), B3 (16,0),观察每次变换前后的三角形有何变化,找出规律,按此变换规律将△OA3B3变换成△OAnBn, ,则An的坐标是_______ ,Bn的坐标是_________ .
.
-
科目: 来源: 题型:
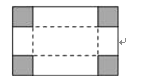
查看答案和解析>>【题目】如图是一块矩形铁皮,将四个角各剪去一个边长为2米的正方形后(剩下的部分做成一个)容积为90立方米的无盖长方体箱子,已知长方体箱子底面积的长比宽多4米,求矩形铁皮的面积.
-
科目: 来源: 题型:
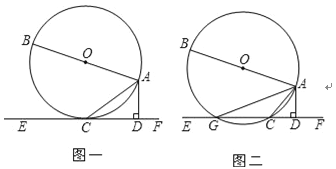
查看答案和解析>>【题目】如图一,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.
(1)求证:∠CAD=∠BAC;
(2)如图二,若把直线EF向上移动,使得EF与⊙O相交于G,C两点(点C在点G的右侧),连接AC,AG,若题中其他条件不变,这时图中是否存在与∠CAD相等的角?若存在,找出一个这样的角,并证明;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】南北朝著名的数学家祖冲之算出圆周率约为3.1415926,在3.1415926这个数中数字“1”出现的频数与频率分别为( )
A. 2,20% B. 2,25% C. 3,25% D. 1,20%
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于a,b的多项式3(a2-2ab-b2)-(a2+mab+2b2)中不含有ab项,则m=________.
相关试题

