【题目】为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式更合算?
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(3)王阿姨每年去该健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.
参考答案:
【答案】
(1)解:35×6=210(元),210<280<560,
∴李叔叔选择普通消费方式更合算
(2)解:根据题意得:y普通=35x.
当x≤12时,y白金卡=280;当x>12时,y白金卡=280+35(x﹣12)=35x﹣140.
∴y白金卡= ![]()
(3)解:当x=18时,y普通=35×18=630;y白金卡=35×18﹣140=490;
令y白金卡=560,即35x﹣140=560,
解得:x=20.
当18≤x≤19时,选择白金卡消费最合算;当x=20时,选择白金卡消费和钻石卡消费费用相同;当x≥21时,选择钻石卡消费最合算
【解析】(1)根据普通消费方式,算出健身6次的费用,再与280、560进行比较,即可得出结论;(2)根据“普通消费费用=35×次数”即可得出y普通关于x的函数关系式;再根据“白金卡消费费用=卡费+超出部分的费用”即可得出y白金卡关于x的函数关系式;(3)先算出健身18次普通消费和白金卡消费两种形式下的费用,再令白金卡消费费用=钻石卡消费的卡费,算出二者相等时的健身次数,由此即可得出结论.本题考查了一次函数的应用,解题的关键是:(1)根据数量关系列式计算;(2)根据数量关系找出函数关系式;(3)令y白金卡=560,算出白金卡消费和钻石卡消费费用相同时健身的次数.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列式计算(或列出函数关系式)是关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,过⊙O上的两点A、B分别作切线,并交BO、AO的延长线于点C、D,连接CD,交⊙O于点E、F,过圆心O作OM⊥CD,垂足为M点.求证:
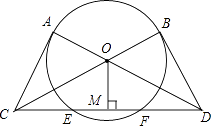
(1)△ACO≌△BDO;
(2)CE=DF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是一片水田,某村民小组需计算其面积,测得如下数据:
∠A=90°,∠ABD=60°,∠CBD=54°,AB=200m,BC=300m.
请你计算出这片水田的面积.
(参考数据:sin54°≈0.809,cos54°≈0.588,tan54°≈1.376,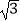 ≈1.732)
≈1.732)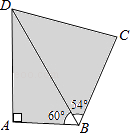
-
科目: 来源: 题型:
查看答案和解析>>【题目】葛藤是一种刁钻的植物,它自己腰杆不硬,为了争夺雨露阳光,常常饶着树干盘旋而上,它还有一手绝招,就是它绕树盘上升的路线,总是沿着最短路线——盘旋前进的。难道植物也懂得数学吗?
阅读以上信息,你能设计一种方法解决下列问题吗?
(1)如图,如果树的周长为3cm,从点A绕一圈到B点,葛藤升高4cm,则它爬行路程是多少厘米?
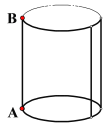
(2)如果树的周长为8cm,绕一圈爬行10cm,则爬行一圈升高多少厘米?如果爬行10圈到达树顶,则树干高多少厘米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,E为CD的中点,H为BE上的一点,
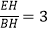 ,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F.
,连接CH并延长交AB于点G,连接GE并延长交AD的延长线于点F. 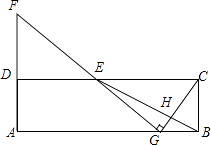
(1)求证: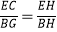 ;
;
(2)若∠CGF=90°,求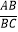 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】尺规作图:某学校正在进行校园环境的改造工程设计,准备在校内一块四边形花坛内栽上一棵桂花树.如图,要求桂花树的位置(视为点P),到花坛的两边AB、BC的距离相等,并且点P到点A、D的距离也相等.请用尺规作图作出栽种桂花树的位置点P(不写作法,保留作图痕迹).

相关试题

