【题目】如图,∠AOB=90°,在∠AOB的内部有一条射线OC.
(1)画射线OD⊥OC.
(2)写出此时∠AOD与∠BOC的数量关系,并说明理由.
参考答案:
【答案】
(1)解:如图所示:
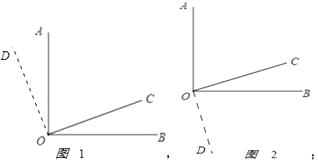
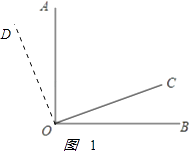
(2)解:如图1:
 ,
,
∠AOD=∠BOC.
因为∠AOB=90°,
所以∠AOC+∠BOC=90°.
因为OD⊥OC,
所以∠AOD+∠AOC=90°.
所以∠AOD=∠BOC;
如图2:
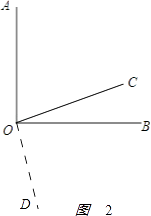 ,
,
∠AOD+∠BOC=180°.
因为∠AOD=∠AOC+∠BOC+∠BOD,
所以∠AOD+∠BOC=∠AOC+∠BOC+∠BOD+∠BOC
=∠AOB+∠COD=180°.
【解析】(1)根据垂线的定义,过直线上一点作已知线的垂线,此题两种情况,垂线作在OC的左边与右边;
(2)此题两种情况,![]() 当OD在OC左边时,根据同角的余角相等得出∠AOD=∠BOC,当OD在OC右边时,根据角的和差得出∠AOD+∠BOC=180°.
当OD在OC左边时,根据同角的余角相等得出∠AOD=∠BOC,当OD在OC右边时,根据角的和差得出∠AOD+∠BOC=180°.
【考点精析】本题主要考查了角的运算和垂线的性质的相关知识点,需要掌握角之间可以进行加减运算;一个角可以用其他角的和或差来表示;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(ab2)3的结果是( )
A.3ab2
B.ab6
C.a3b5
D.a3b6 -
科目: 来源: 题型:
查看答案和解析>>【题目】“三次投掷一枚硬币,三次正面朝上”这一事件是( )
A. 必然事件 B. 随机事件 C. 不可能事件 D. 确定事件
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,从该地区随机抽取部分七年级学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名同学只能选择其中一类节目),并调查得到的数据用下面的表和扇形图来表示(表、图都没制作完成)

根据表、图提供的信息,解决以下问题:
(1)计算出表中a、b的值;
(2)求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数;
(3)若该地区七年级学生共有47500人,试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人?

-
科目: 来源: 题型:
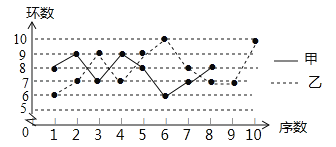
查看答案和解析>>【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:

且
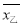 =8,
=8,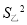 =1.8,根据上述信息完成下列问题:
=1.8,根据上述信息完成下列问题:(1)将甲运动员的折线统计图补充完整;
(2)乙运动员射击训练成绩的众数是 ,中位数是 .
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
-
科目: 来源: 题型:
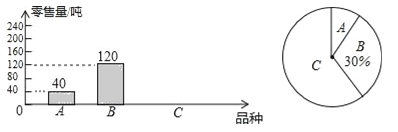
查看答案和解析>>【题目】为了解茂名某水果批发市场荔枝的销售情况,某部门对该市场的三种荔枝品种A、B、C在6月上半月的销售进行调查统计,绘制成如下两个统计图(均不完整).请你结合图中的信息,解答下列问题:
(1)该市场6月上半月共销售这三种荔枝多少吨?
(2)该市场某商场计划六月下半月进货A、B、C三种荔枝共500千克,根据该市场6月上半月的销售情况,求该商场应购进C品种荔枝多少千克比较合理?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若多项式x2+px+12可分解为两个一次因式的积,则整数p可能的取值有( )
A. 3个 B. 4个 C. 5个 D. 6个
相关试题

