练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

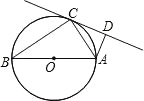
    【题目】如图，AB是⊙O的直径，C是⊙O上一点，∠ACD=∠B，AD⊥CD．

    （1）求证：CD是⊙O的切线；

    （2）若AD=1，OA=2，求AC的值．

    【答案】（1）证明见解析；（2）2.

    【解析】

    试题分析：（1）连接OC，易知∠ACB=90°. ∠B=∠BCO，可推出∠OCD=90°，可得出结论；（2）可证△ACB∽△ADC，利用对应边成比例可求得AC的值.

    试题解析：（1）证明：连接OC，∵AB是⊙O直径，∴∠ACB=90°，∵OB=OC，∴∠B=∠BCO，又∵∠ACD=∠B，

    ∴∠OCD=∠OCA+∠ACD=∠OCA+∠BCO=∠ACB=90°，即OC⊥CD，∴CD是⊙O的切线；（2）解：∵AD⊥CD，

    ∴∠ADC=∠ACB=90°，又∵∠ACD=∠B，∴△ACB∽△ADC，∴，∴AC2=ADAB=1×4=4，∴AC=2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】(2016山东潍坊第24题)如图，在菱形ABCD中，AB=2，∠BAD=60°，过点D作DE⊥AB于点E，DF⊥BC于点F．

    （1）如图1，连接AC分别交DE、DF于点M、N，求证：MN=AC；

    （2）如图2，将△EDF以点D为旋转中心旋转，其两边DE′、DF′分别与直线AB、BC相交于点G、P，连接GP，当△DGP的面积等于3时，求旋转角的大小并指明旋转方向．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算中，正确的是（　　）

    A.x3+x3=x6B.x3x6=x18C.（x2）3=x5D.x2÷x=x

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，以AB为直径的⊙O分别于BC，AC相交于点D，E，BD=CD，过点D作⊙O的切线交边AC于点F．

    （1）求证：DF⊥AC；

    （2）若⊙O的半径为5，∠CDF=30°，求的长（结果保留π）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列各式中，表示y是x的正比例函数的是（　　）

    A.y=2x-1B.y=2xC.y2=2xD.y=2x2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一次函数y=kx+b满足kb＞0，且y随x的增大而减小，则此函数的图象不经过（　　）

    A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列计算正确的是（ ）
    A.a2a3=a6
    B.（﹣m2）3=﹣m6
    C.b6÷b3=b2
    D.3a+3b=6ab

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点（3，2）关于y轴对称点为（　　）

    A. （﹣3，2） B. （3，﹣2） C. （2，﹣3） D. （3，﹣2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若x+2y＝5，则代数式3﹣x﹣2y的值为（ ）

    A.﹣8B.﹣2C.2D.8

    查看答案和解析>>

    同步练习册答案