【题目】连接AB,直线AB与x轴交于点C,与y轴交于点D,平面内有一点E(3,1),直线BE与x轴交于点F.直线AB的解析式记作y1=kx+b,直线BE解析式记作y2=mx+t.求:
(1)直线AB的解析式△BCF的面积;
(2)当x 时,kx+b>mx+t;
当x 时,kx+b<mx+t;
当x 时,kx+b=mx+t;
(3)在x轴上有一动点H,使得△OBH为等腰三角形,求H的坐标.
参考答案:
【答案】(1)![]() .(2)>2;<2;=2.(3)(-
.(2)>2;<2;=2.(3)(-![]() ,0)、(
,0)、(![]() ,0)、(4,0)或(
,0)、(4,0)或(![]() ,0).
,0).
【解析】
试题分析:(1)根据观察图象可以找出点B、C、D的坐标,根据待定系数法即可求出直线AB、BE的解析式,令y2=0即可求出点F的坐标,结合三角形的面积公式即可得出结论;
(2)当直线AB的图象在直线BE图象上方时,有kx+b>mx+t;当直线AB的图象在直线BE图象下方时,有kx+b<mx+t;二者相交时,有kx+b=mx+t.结合图象即可得出结论;
(3)设点H的坐标为(n,0),用两点间的距离公式找出OB、OH、BH的长度,结合△OBH为等腰三角形的三种情况,即可求出n的值.
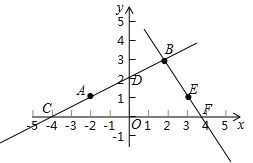
试题解析:(1)观察函数图象可知:
点C(-4,0),点D(0,2),点B(2,3),
将C、D点坐标代入直线AB的解析式中,得![]() ,
,
解得:![]() .
.
∴直线AB的解析式为y1=![]() x+2.
x+2.
将点B(2,3),E(3,1)代入到直线BE的解析式中,得![]() ,
,
解得:![]() .
.
∴直线BE的解析式为y2=-2x+7.
令y2=0,则有-2x+7=0,解得m=![]() ,
,
即点F的坐标为(![]() ,0).
,0).
∴CF=![]() -(-4)=
-(-4)=![]() ,
,
∴△BCF的面积S=![]() ×3CF=
×3CF=![]() ×3×
×3×![]() =
=![]() .
.
(2)结合函数图象可知:
当x>2时,kx+b>mx+t;当x<2时,kx+b<mx+t;当x=2时,kx+b=mx+t.
(3)设点H的坐标为(n,0).
∵点O(0,0),点B(2,3),
∴OB=![]() ,OH=|n|,BH=
,OH=|n|,BH=![]() .
.
△OBH为等腰三角形分三种情况:
①当OB=OH时,即![]() =|n|,解得:n=±
=|n|,解得:n=±![]() ,
,
此时点H的坐标为(-![]() ,0)或(
,0)或(![]() ,0);
,0);
②当OB=BH时,即![]() =
=![]() ,解得:n=0(舍去),或n=4.
,解得:n=0(舍去),或n=4.
此时点H的坐标为(4,0);
③当OH=BH时,即|n|=![]() ,解得:n=
,解得:n=![]() .
.
此时点H的坐标为(![]() ,0).
,0).
综上可知:点H的坐标为(-![]() ,0)、(
,0)、(![]() ,0)、(4,0)或(
,0)、(4,0)或(![]() ,0).
,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】钢笔每支a元,铅笔每支b元,小明买3支钢笔和2支铅笔共需______元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】回答下列问题:
(1)计算:①(x+2)(x+3)=__ ___;② (x +7)( x-10)=___ _;③(x-5)(x-6)=_ __.
(2)由(1)的结果,直接写出下列计算的结果:
①(x+1)(x+3)=___ ___;②(x-2)(x-3)=__ ____;
③(x+2)(x-5)=__ _;
(3)总结公式:(x+a) (x+b)=______ ______.
(4)已知a,b,m均为整数,且(x+a)(x+b)=
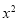 +mx+6,求m的所有可能值.
+mx+6,求m的所有可能值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为美化小区环境,某小区有一块面积为30m2的等腰三角形草地,测得其一边长为10m,现要给这块三角形草地围上白色的低矮栅栏,则其长度为 m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形不具备的性质是( )
A. 四条边都相等 B. 对角线一定相等 C. 是轴对称图形 D. 是中心对称图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个只含有字母a的二次三项式,它的二次项系数,一次项系数均为﹣3,常数项为1,则这个多项式为______
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过观察你能肯定的是( )
A. 图形中线段是否相等 B. 图形中线段是否平行
C. 图形中线段是否相交 D. 图形中线段是否垂直
相关试题

