【题目】学校组织师生开展植树造林活动,为了了解全校4000名学生的情况,随机抽样调查50名学生的植树情况,制成如下统计表和条形统计图(均不完整)。

(1)将统计表和条形统计图补充完整;
(2)求抽样的50名学生植树数量的平均数;
(3)根据抽样数据,估计该校4000名学生的植树数量。
参考答案:
【答案】(1)答案见解析;(2)4.6棵;(3)18400棵.
【解析】
试题分析:(1)用总人数减去其他小组的人数即可求得植树棵树为5的小组的频数,除以总人数即可得到该组的频率;
(2)用加权平均数计算植树量的平均数即可;
(3)用样本的平均数估计总体的平均数即可.
试题解析:1)统计表和条形统计图补充如下:
植树量为5棵的人数为:50-5-20-10=15,频率为:15÷50=0.3,,

(2)抽样的50名学生植树的平均数是:![]() =4.6(棵).
=4.6(棵).
(3)∵样本数据的平均数是4.6,
∴估计该校4000名学生参加这次植树活动的总体平均数是4.6棵.
于是4.6×4000=18400(棵),
∴估计该校800名学生植树约为18400棵.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电信公司最近开发A、B两种型号的手机,一经营手机专卖店销售A、B两种型号的手机,上周销售1部A型3部B型的手机,销售额为8400元.本周销售2部A型1部B型的手机,销售额为5800元.
(1)求每部A型和每部B型手机销售价格各是多少元?
(2)如果某单位拟向该店购买A、B两种型号的手机共6部,发给职工联系业务,购手机费用不少于11200元且不多于11600元,问有哪几种购买方案?
(3)在(2)中哪种方案费用更省?最少费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式ab﹣2ab2﹣a的次数为________
-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形的内角和等于( )
A.90° B.180° C.300° D.360°
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
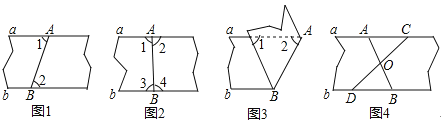
A.如图1,展开后测得∠1=∠2
B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2
D.如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
-
科目: 来源: 题型:
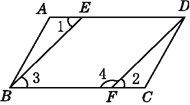
查看答案和解析>>【题目】如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:
解:因为AD∥BC(已知),
所以∠1=∠3(__________________________________).
因为∠1=∠2(已知),
所以∠2=∠3.
所以BE∥__________ (______________________________________).
所以∠3+∠4=180°(______________________________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=
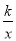 (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .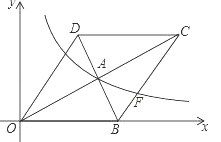
相关试题

