【题目】已知抛物线![]() ,直线
,直线![]() 的对称轴与
的对称轴与![]() 交于点
交于点![]() ,点
,点![]() 与
与![]() 的顶点
的顶点![]() 的距离是4.
的距离是4.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 随着
随着![]() 的增大而增大,且
的增大而增大,且![]() 与
与![]() 都经过
都经过![]() 轴上的同一点,求
轴上的同一点,求![]() 的解析式.
的解析式.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 或者
或者![]()
【解析】
试题分析:(1)利用二次函数的对称轴公式求出m,再利用两点间的距离公式求出n;(2)根据一次函数的性质求出k大于0,注意分类讨论解决问题,用待定系数法求一次函数的表达式.
试题解析:(1)![]() 的对称轴与
的对称轴与![]() 的交点为
的交点为![]()
![]() 的对称轴为
的对称轴为![]() ,
,![]()
![]()
![]() 顶点坐标为
顶点坐标为![]()
![]()
![]()
![]()
(2)①当![]() 时,
时,![]() 与
与![]() 轴交点为
轴交点为![]()
![]() 随
随![]() 的增大而增大.
的增大而增大.
![]()
i.当![]() 经过点
经过点![]() 时
时
则有![]()
![]()
![]() (不符,舍去)
(不符,舍去)
ii.当![]() 经过点
经过点![]() 时
时
则有![]()
![]()
②当![]() 时,令
时,令![]() 则
则![]() ,则
,则![]()
![]() 与
与![]() 轴交于点
轴交于点![]()
i.当![]() 经过点
经过点![]() 时
时
则有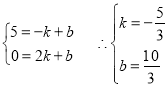
![]()
![]() (不符,舍去)
(不符,舍去)
ii.当![]() 经过点
经过点![]() 时
时
则有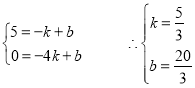
![]()
综上述,![]() 或者
或者![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家草莓采摘园的草莓品质相同,销售价格也相同.“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买60元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.
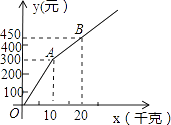
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克元;
(2)求y1、y2与x的函数表达式;
(3)在图中画出y1与x的函数图象,并写出选择甲采摘园所需总费用较少时,草莓采摘量x的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3×(1﹣3)+16÷(﹣2)3﹣(﹣5)
-
科目: 来源: 题型:
查看答案和解析>>【题目】绝对值大于2且小于5的所有整数的和是( )
A.0
B.7
C.14
D.28 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a2﹣2a=3,则﹣3a2+6a+2019=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边上一点,E是AD的中点,过A作BC的平行线交CE的延长线F,且AF=BD,连结BF.
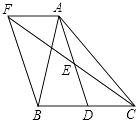
(1)求证:BD=CD;
(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论;
(3)当△ABC满足什么条件时,四边形AFBD为正方形?(写出条件即可,不要求证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】有5根小木棒,长度分别为2cm、3cm、4cm、5cm、6cm,任意取其中的3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为( )
A.5个B.6个C.7个D.8个
相关试题

