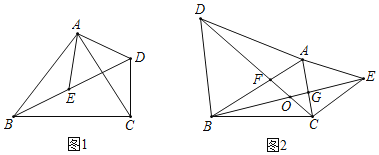
【题目】(1)问题发现:如图1,如果△ABC和△ADE均为等边三角形(等边三角形的三条边都相等,三个角都是60°),点B、E、D三点在同一直线上,连接CD.则CD与BE的数量关系为______;∠BDC的度数为______度.
(2)探究:如图2,若△ABC为三边互不相等的三角形,以它的边AB、AC为边分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,则CD与BE还相等吗?若相等,请证明,若不相等,说明理由:并请求出∠BOD的度数?
参考答案:
【答案】(1)相等,60;(2)CD=BE ;∠BOD=60°.
【解析】
(1)由条件△ABC和△ADE均为等边三角形,易证△ABE≌△ACD,从而得到对应边相等,即CD=BE;由△ABE≌△ACD,可得∠BEA=∠CDA,由点B,D,E在同一直线上,可求出∠BEA=120°,从而可以求出∠BDC的度数;
(2)根据等边三角形的性质和全等三角形的判定和性质得出CD=BE,∠ADC=∠ABE,进而解答即可.
(1)∵△ABC和△ADE均为等边三角形,
∴AB=AC,AE=AD,∠BAC=∠EAD=60°,
∴∠BAE=∠CAD.
在△ABE和△ACD中,
∵ ,
,
∴△ABE≌△ACD(SAS),
∴CD=BE,
∵△ABE≌△ACD,
∴∠BEA=∠CDA,
∵△AED为等边三角形,
∴∠AED=∠ADE=60°,
∵点B,D,E在同一直线上,
∴∠BEA=120°,
∴∠CDA=120°,
∴∠BDC=∠CDA-∠ADE=60°,
(2)∵以AB、AC为边分别向外做等边△ABD和等边△ACE,
∴AD=AB,AE=AC,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
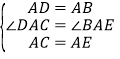 ,
,
∴△DAC≌△BAE(SAS)
∴CD=BE,∠ADC=∠ABE,
∵∠ABE+∠BFO+∠BOD=∠ADC+∠AFD+∠BAD=180°,
又∠BFO=∠AFD,∠ADC=∠ABE
∴∠BOD=∠BAD=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如:
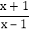 =
= =
=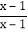 +
+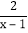 =1+
=1+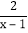 ,
,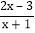 =
=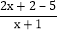 =
=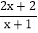 +
+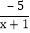 =2+
=2+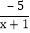 ,则
,则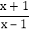 和
和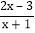 都是“和谐分式”.
都是“和谐分式”.(1)下列分式中,属于“和谐分式”的是______(填序号);
①
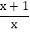 ;②
;②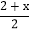 ;③
;③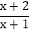 ;④
;④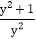
(2)将“和谐分式”
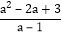 化成一个整式与一个分子为常数的分式的和的形式为:
化成一个整式与一个分子为常数的分式的和的形式为: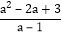 =______+______;
=______+______;(3)应用:先化简
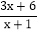 -
-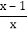 ÷
÷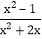 ,并求x取什么整数时,该式的值为整数.
,并求x取什么整数时,该式的值为整数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.

(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】山地自行车越来越受中学生的喜爱.一网店经营的一个型号山地自行车,今年一月份销售额为30000元,二月份每辆车售价比一月份每辆车售价降价100元,若销售的数量与上一月销售的数量相同,则销售额是27000元.
(1)求二月份每辆车售价是多少元?
(2)为了促销,三月份每辆车售价比二月份每辆车售价降低了10%销售,网店仍可获利35%,求每辆山地自行车的进价是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB∥CD,点E为AB,CD之外任意一点.
(1)如图1,探究∠BED与∠B,∠D的数量关系,并说明理由;
(2)如图2,探究∠CDE与∠B,∠E的数量关系,并说明理由.
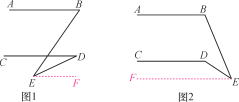
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
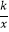 与一次函数y=ax+b的图象交于点A(2,2)、B(
与一次函数y=ax+b的图象交于点A(2,2)、B(  ,n).
,n). 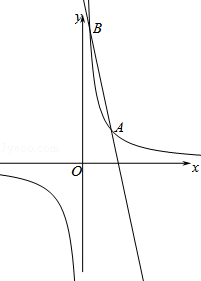
(1)求这两个函数解析式;
(2)将一次函数y=ax+b的图象沿y轴向下平移m个单位,使平移后的图象与反比例函数y=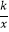 的图象有且只有一个交点,求m的值.
的图象有且只有一个交点,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
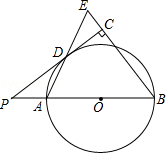
(1)求证:AB=BE;
(2)若PA=2,cosB=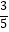 ,求⊙O半径的长.
,求⊙O半径的长.
相关试题

