【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,动点P从点A出发,以1cm/s的速度向点D运动;动点Q从点C同时出发,以3cm/s的速度向点B运动.规定当其中一个动点到达端点时,另一个动点也随之停止运动.设运动时间为t,求: 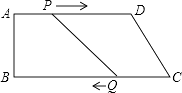
(1)当t为何值时,PQ∥CD?
(2)当t为何值时,PQ=CD?
参考答案:
【答案】
(1)解:根据题意得:PA=t,CQ=3t,则PD=AD﹣PA=24﹣t,
∵AD∥BC,即PD∥CQ,
∴当PD=CQ时,四边形PQCD为平行四边形,
∴PQ∥CD,
即24﹣t=3t,
解得:t=6,
即当t=6时,PQ∥CD
(2)解:若要PQ=CD,分为两种情况:
①当四边形PQCD为平行四边形时,
即PD=CQ
24﹣t=3t,
解得:t=6,
②当四边形PQCD为等腰梯形时,
即CQ=PD+2(BC﹣AD)
3t=24﹣t+4
解得:t=7,
即当t=6或t=7时,PQ=CD
【解析】(1)由当PQ∥CD时,四边形PQCD为平行四边形,可得方程24﹣t=3t,解此方程即可求得答案;(2)根据PQ=CD,一种情况是:四边形PQCD为平行四边形,可得方程24﹣t=3t,一种情况是:四边形PQCD为等腰梯形,可求得当QC﹣PD=QC﹣EF=QF+EC=2CE,即3t=(24﹣t)+4时,四边形PQCD为等腰梯形,解此方程即可求得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,Rt△ABC中,∠ACB=Rt∠,AC=8,BC=6,点D为AB的中点,动点P从点A出发,沿AC方向以每秒1个单位的速度向终点C运动,同时动点Q从点C出发,以每秒2个单位的速度先沿CB方向运动到点B,再沿BA方向向终点A运动,以DP,DQ为邻边构造PEQD,设点P运动的时间为t秒.
(1)当t=2时,求PD的长;
(2)如图2,当点Q运动至点B时,连结DE,求证:DE∥AP.
(3)如图3,连结CD.
①当点E恰好落在△ACD的边上时,求所有满足要求的t值;
②记运动过程中PEQD的面积为S,PEQD与△ACD的重叠部分面积为S1,当
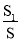 <
<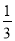 时,请直接写出t的取值范围是 ______ .
时,请直接写出t的取值范围是 ______ .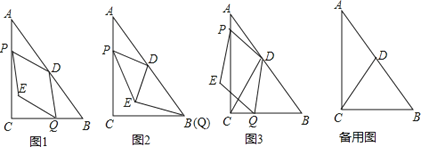
-
科目: 来源: 题型:
查看答案和解析>>【题目】证明一个四边形是正方形,使用次数最少的方法对折,则应该对折( )
A.1次B.2次C.3次D.4次
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上点A表示的数为a,点B表示的数为b,且a,b满足|a+2|+(3a+b)2=0,O为原点.

(1)则a= ,b= ;
(2)若动点P从点A出发,以每秒1个单位长度的速度沿数轴向右匀速运动,
①当PO=2PB时,求点P的运动时间t;
②当点P运动到线段OB上时,分别取AP和OB的中点E、F,则
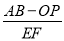 的值是否为一个定值?如果是,求出定值,如果不是,说明理由.
的值是否为一个定值?如果是,求出定值,如果不是,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】五个城市的国际标准时间(单位:时)在数轴上表示如图所示.对应于北京时间2009年1月1日上午10时这一时刻,下列说法错误的是( )
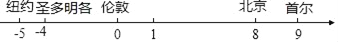
A. 伦敦时间为2009年1月1日凌晨2时
B. 纽约时间为2008年12月31日晚上20时
C. 圣多明各时间为2008年12月31日晚上22时
D. 首尔时间为2009年1月1日上午11时
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=
 (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(-2,0),则下列结论中,正确的是( )
A.b=2a+k B.a=b+k C.a>b>0 D.a>k>0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC与BD交于点O,AC=6,BD=8.动点E从点B出发,沿着B﹣A﹣D在菱形ABCD的边上运动,运动到点D停止.点F是点E关于BD的对称点,EF交BD于点P,若BP=x,△OEF的面积为y,则y与x之间的函数图象大致为( )

A.
 B.
B. 
C.
 D.
D. 
相关试题

