【题目】如图,已知正方形ABCD的边长为4,对称中心为点P,点F为BC边上一个动点,点E在AB边上,且满足条件∠EPF=45°,图中两块阴影部分图形关于直线AC成轴对称,设它们的面积和为S1 . 
(1)求证:∠APE=∠CFP;
(2)设四边形CMPF的面积为S2 , CF=x, ![]() .
.
①求y关于x的函数解析式和自变量x的取值范围,并求出y的最大值;
②当图中两块阴影部分图形关于点P成中心对称时,求y的值.
参考答案:
【答案】
(1)
证明:∵∠EPF=45°,
∴∠APE+∠FPC=180°﹣45°=135°;
而在△PFC中,由于PC为正方形ABCD的对角线,则∠PCF=45°,
则∠CFP+∠FPC=180°﹣45°=135°,
∴∠APE=∠CFP
(2)
解:①∵∠APE=∠CFP,且∠FCP=∠PAE=45°,
∴△APE∽△CFP,则 ![]() .
.
而在正方形ABCD中,AC为对角线,则AC= ![]() AB=
AB= ![]() ,
,
又∵P为对称中心,则AP=CP= ![]() ,
,
∴AE= ![]() =
= ![]() =
= ![]() .
.
如图,过点P作PH⊥AB于点H,PG⊥BC于点G,
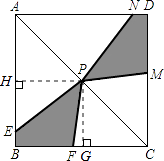
P为AC中点,则PH∥BC,且PH= ![]() BC=2,同理PG=2.
BC=2,同理PG=2.
S△APE= ![]() =
= ![]() ×2×
×2× ![]() =
= ![]() ,
,
∵阴影部分关于直线AC轴对称,
∴△APE与△APN也关于直线AC对称,
则S四边形AEPN=2S△APE= ![]() ;
;
而S2=2S△PFC=2× ![]() =2x,
=2x,
∴S1=S正方形ABCD﹣S四边形AEPN﹣S2=16﹣ ![]() ﹣2x,
﹣2x,
∴y= ![]() =
= ![]() =
= ![]() +
+ ![]() ﹣1.
﹣1.
∵E在AB上运动,F在BC上运动,且∠EPF=45°,
∴2≤x≤4.
令 ![]() =a,则y=﹣8a2+8a﹣1,当a=
=a,则y=﹣8a2+8a﹣1,当a= ![]() =
= ![]() ,即x=2时,y取得最大值.
,即x=2时,y取得最大值.
而x=2在x的取值范围内,代入x=2,则y最大=4﹣2﹣1=1.
∴y关于x的函数解析式为:y= ![]() +
+ ![]() ﹣1(2≤x≤4),y的最大值为1.
﹣1(2≤x≤4),y的最大值为1.
②图中两块阴影部分图形关于点P成中心对称,
而此两块图形也关于直线AC成轴对称,则阴影部分图形自身关于直线BD对称,
则EB=BF,即AE=FC,
∴ ![]() =x,解得x=
=x,解得x= ![]() ,
,
代入x= ![]() ,得y=
,得y= ![]() ﹣2.
﹣2.
【解析】(1)利用正方形与三角形的相关角之间的关系可以证明结论;
(2)本问关键是求出y与x之间的函数解析式.①首先分别用x表示出S1与S2 , 然后计算出y与x的函数解析式.这是一个二次函数,求出其最大值;②注意中心对称、轴对称的几何性质.
【考点精析】本题主要考查了相似三角形的性质的相关知识点,需要掌握对应角相等,对应边成比例的两个三角形叫做相似三角形才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某公司有三个住宅区可看作一点,A,B,C各区分别住有职工30人、15人、10人,且这三个住宅区在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )

A. 点A B. 点B
C. A,B之间 D. B,C之间
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班有50位学生,每位学生都有一个序号,将50张编有学生序号(从1号到50号)的卡片(除序号不同外其它均相同)打乱顺序重新排列,从中任意抽取1张卡片.
(1)在序号中,是20的倍数的有:20,40,能整除20的有:1,2,4,5,10(为了不重复计数,20只计一次),求取到的卡片上序号是20的倍数或能整除20的概率;
(2)若规定:取到的卡片上序号是k(k是满足1≤k≤50的整数),则序号是k的倍数或能整除k(不重复计数)的学生能参加某项活动,这一规定是否公平?请说明理由;
(3)请你设计一个规定,能公平地选出10位学生参加某项活动,并说明你的规定是符合要求的. -
科目: 来源: 题型:
查看答案和解析>>【题目】

(1)先求解下列两题: ①如图①,点B,D在射线AM上,点C,E在射线AN上,且AB=BC=CD=DE,已知∠EDM=84°,求∠A的度数;
②如图②,在直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B,C的横坐标都是3,且BC=2,点D在AC上,且横坐标为1,若反比例函数 的图象经过点B,D,求k的值.
的图象经过点B,D,求k的值.
(2)解题后,你发现以上两小题有什么共同点?请简单地写出. -
科目: 来源: 题型:
查看答案和解析>>【题目】一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是( )

A.5:4
B.5:2
C. :2
:2
D. :
: 
-
科目: 来源: 题型:
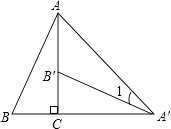
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )
A.70°
B.65°
C.60°
D.55° -
科目: 来源: 题型:
查看答案和解析>>【题目】学校开展“阳光体育”活动,学生会为了解学生最喜欢哪一种球类运动项目,
 :足球、
:足球、 :乒乓球、
:乒乓球、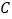 :篮球、
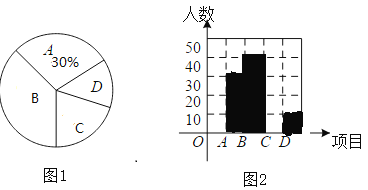
:篮球、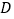 :羽毛球,随机抽取了一部分学生进行调查(要求每位同学只能选择一种喜欢的球类),并将调查结果绘制成如下两个不完整的统计图,如图1,图2,请你根据图中提供的信息解答下列问题。
:羽毛球,随机抽取了一部分学生进行调查(要求每位同学只能选择一种喜欢的球类),并将调查结果绘制成如下两个不完整的统计图,如图1,图2,请你根据图中提供的信息解答下列问题。(1)在这次调查中,一共调查了_____名学生;
(2)在图1扇形统计图中,求出“
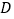 ”部分所对应的圆心角等于_____度;
”部分所对应的圆心角等于_____度;(3)求喜欢篮球的同学占被抽查人数的百分比,并补全频数分布折线统计图.
相关试题

