【题目】在一个不透明的袋子中放有若干个球,其中有6个白球,其余是红球,这些球除颜色外完全相同.每次把球充分搅匀后,任意摸出一个球记下颜色再放回袋子.通过大量重复试验后,发现摸到白球的频率稳定在0.25左右,则红球的个数约是( )
A.2B.12C.18D.24
参考答案:
【答案】C
【解析】
根据用频率估计概率可知: 摸到白球的概率为0.25,根据概率公式即可求出小球的总数,从而求出红球的个数.
解:小球的总数约为:6÷0.25=24(个)
则红球的个数为:24-6=18(个)
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在学校开展的“争做最优秀中学生”的一次演讲比赛中,编号1,2,3,4,5的五位同学最后成绩如表所示:那么这五位同学演讲成绩的众数与中位数依次是( )
参赛者编号
1
2
3
4
5
成绩/分
96
88
86
93
86
A.96,88
B.86,88
C.88,86
D.86,86 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形
 的顶点
的顶点  的坐标为
的坐标为  ,动点
,动点  从原点
从原点  出发,以每秒
出发,以每秒  个单位的速度沿折线
个单位的速度沿折线  运动,到点
运动,到点  时停止,同时,动点
时停止,同时,动点  从点
从点  出发,以每秒
出发,以每秒  个单位的速度在线段
个单位的速度在线段  上运动,当一个点停止时,另一个点也随之停止.在运动过程中,当线段
上运动,当一个点停止时,另一个点也随之停止.在运动过程中,当线段  恰好经过点
恰好经过点  时,运动时间
时,运动时间  的值是 .
的值是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点
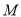 在以
在以 为圆心,
为圆心,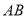 为直径的半圆弧上运动(点
为直径的半圆弧上运动(点 不与点
不与点 及
及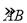 的中点
的中点 重合),连接
重合),连接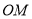 .过点
.过点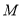 作
作 于点
于点 ,以
,以 为边在半圆同侧作正方形
为边在半圆同侧作正方形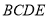 ,过
,过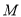 点作
点作 的切线交射线
的切线交射线 于点
于点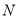 ,连接
,连接 、
、 .
.(1)探究:如左图,当
 动点在
动点在 上运动时;
上运动时;①判断
 是否成立?请说明理由;
是否成立?请说明理由; ②设
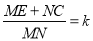 ,
, 是否为定值?若是,求出该定值,若不是,请说明理由;
是否为定值?若是,求出该定值,若不是,请说明理由;③设
 ,
,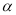 是否为定值?若是,求出该定值,若不是,请说明理由;
是否为定值?若是,求出该定值,若不是,请说明理由;(2)拓展:如右图,当动点
 在
在 上运动时;
上运动时;分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点O是正方形ABCD对角线BD的中点.
(1)如图1,若点E是OD的中点,点F是AB上一点,且使得∠CEF=90°,过点E作ME∥AD,交AB于点M,交CD于点N.
①∠AEM=∠FEM; ②点F是AB的中点;
(2)如图2,若点E是OD上一点,点F是AB上一点,且使
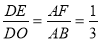 ,请判断△EFC的形状,并说明理由;
,请判断△EFC的形状,并说明理由;(3)如图3,若E是OD上的动点(不与O,D重合),连接CE,过E点作EF⊥CE,交AB于点F,当
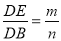 时,请猜想
时,请猜想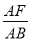 的值(请直接写出结论).
的值(请直接写出结论).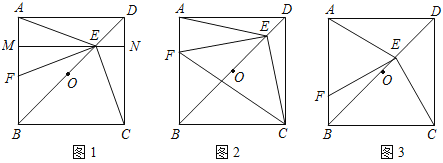
-
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣4x﹣3向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )
A.y=(x+1)2﹣2
B.y=(x﹣5)2﹣2
C.y=(x﹣5)2﹣12
D.y=(x+1)2﹣12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+1经过A(-1,0),B(1,1)两点.
(1)求该抛物线的解析式;
(2)阅读理解:
在同一平面直角坐标系中,直线l1:y=k1x+b1(k1,b1为常数,且k1≠0),直线l2:y=k2x+b2(k2,b2为常数,且k2≠0),若l1⊥l2,则k1·k2=-1.
解决问题:
①若直线y=3x-1与直线y=mx+2互相垂直,求m的值;
②是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)M是抛物线上一动点,且在直线AB的上方(不与A,B重合),求点M到直线AB的距离的最大值.

相关试题

