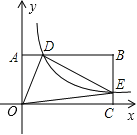
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的两边
的两边![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,反比例函数
轴的正半轴上,反比例函数![]() (
(![]() >0)与
>0)与![]() 相交于点
相交于点![]() ,与
,与![]() 相交于点
相交于点![]() ,若
,若![]() ,且
,且![]() 的面积是5,则
的面积是5,则![]() 的值为_______.
的值为_______.

参考答案:
【答案】![]()
【解析】试题分析:设B点的坐标为(a,b),根据矩形的性质以及BE=4EC,表示出E、D两点的坐标,根据S△ODE=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=5,求出B的横纵坐标的积,进而求出反比例函数的比例系数.
解:∵四边形OCBA是矩形,
∴AB=OC,OA=BC,
设B点的坐标为(a,b),
∵BE=4EC,
∴E(a,![]() b),
b),
∵点D,E在反比例函数的图象上,
∴a![]()
![]() b=k,∴D(
b=k,∴D(![]() a,b),
a,b),
∵S△ODE=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE
=ab﹣![]()
![]() a
a![]() b﹣
b﹣![]()
a![]()
![]() b﹣
b﹣![]() (a﹣
(a﹣![]() a)
a)![]() (b﹣
(b﹣![]() b)
b)
=![]() ab=5,
ab=5,
∴ab=![]() ,
,
∴k=![]() ab=
ab=![]() .
.
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣x﹣1=0根的判别式的值等于
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市2010年元旦这天的最高气温是8℃,最低气温是﹣2℃,则这天的最高气温比最低气温高( )
A.10℃
B.﹣10℃
C.6℃
D.﹣6℃ -
科目: 来源: 题型:
查看答案和解析>>【题目】请写出一个解为x=-3的一元一次方程,结果是____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分
 分)已知在平面直角坐标系
分)已知在平面直角坐标系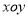 中,点
中,点 是抛物线
是抛物线 上的一个动点,点
上的一个动点,点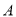 的坐标为
的坐标为 .
.(1).如图1,直线
 过点
过点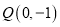 且平行于
且平行于 轴,过
轴,过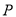 点作
点作 ,垂足为
,垂足为 ,连接
,连接 ,猜想
,猜想 与
与 的大小关系:
的大小关系:  ______
______  (填写“>”“<”或“=” ),并证明你的猜想.
(填写“>”“<”或“=” ),并证明你的猜想.(2).请利用(1)的结论解决下列问题:
①.如图2,设点
 的坐标为
的坐标为 , 连接
, 连接 ,问
,问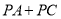 是否存在最小值?如果存在,请说明理由,并求出点
是否存在最小值?如果存在,请说明理由,并求出点 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.②.若过动点
 和点
和点 的直线交抛物线于另一点
的直线交抛物线于另一点 ,且
,且 ,求直线
,求直线 的解析式(图3为备用图).
的解析式(图3为备用图). 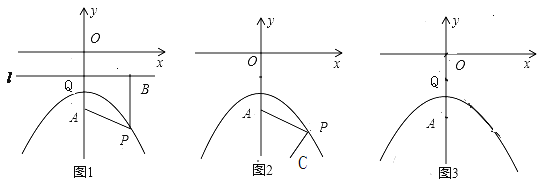
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式a-3b+c-2d的后3项用括号括起来,且括号前面带“-”号,所得结果是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算: 2x-(-3x)=__________,
相关试题

