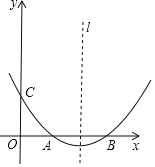
【题目】如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,﹣![]() ),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)
),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)
(1)求抛物线的解析式及A,B两点的坐标;
(2)若(1)中抛物线的对称轴上有点P,使△ABP的面积等于△ABC的面积的2倍,求出点P的坐标;
(3)在(1)中抛物线的对称轴l上是否存在一点Q,使AQ+CQ的值最小?若存在,求AQ+CQ的最小值;若不存在,请说明理由.
参考答案:
【答案】(1)抛物线的解析式为y=![]() (x﹣4)2﹣
(x﹣4)2﹣![]() ,A(2,0),B(6,0);
,A(2,0),B(6,0);
(2)点P坐标(4,4)或(4,﹣4);
(3)存在,QA+QC的最小值为![]() .
.
【解析】(1)抛物线的顶点坐标为(4,﹣![]() ),可以假设抛物线为y=a(x﹣4)2﹣
),可以假设抛物线为y=a(x﹣4)2﹣![]() 把点(0,2)代入得到a=
把点(0,2)代入得到a=![]() ,
,
∴抛物线的解析式为y=![]() (x﹣4)2﹣
(x﹣4)2﹣![]() .
.
令y=0得到![]() (x﹣4)2﹣
(x﹣4)2﹣![]() =0,解得x=2或6,
=0,解得x=2或6,
∴A(2,0),B(6,0).
(2)设P(4,m),
由题意:![]() 4|m|=2×
4|m|=2×![]() ×4×2,解得m=±4,
×4×2,解得m=±4,
∴点P坐标(4,4)或(4,﹣4).
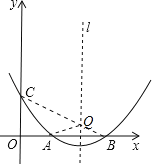
(3)存在.理由如下:
∵A、B关于对称轴对称,连接CB交对称轴于Q,连接QA,此时QA+QC最短(两点之间线段最短),
∴QA+QC的最小值=QA+QC=QB+QC=BC=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】飞机无风时的航速为a千米/时,风速为20千米/时,若飞机顺风飞行3小时,再逆风飞行4小时,则两次行程总共飞行_____千米(用含a的式子表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果+30m表示向东走30m,那么向西走40m表示为( )
A.+40m
B.﹣40m
C.+30m
D.﹣30m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠B=∠C.若AD∥BC,则AD平分∠EAC吗?请说明理由.
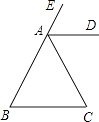
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读解题过程,回答问题.
如图,OC在∠AOB内,∠AOB和∠COD都是直角,且∠BOC=30°,求∠AOD的度数.
解:过O点作射线OM,使点M,O,A在同一直线上.
因为∠MOD+∠BOD=90°,∠BOC+∠BOD=90°,所以∠BOC=∠MOD,
所以∠AOD=180°-∠BOC=180°-30°=150°.
(1)如果∠BOC=60°,那么∠AOD等于多少度?如果∠BOC=n°,那么∠AOD等于多少度?
(2)如果∠AOB=∠DOC=x°,∠AOD=y°,求∠BOC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式2x+5>4x﹣1的正整数解是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车间有22名工人,每人每天可以生产600个螺钉或1000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应如何安排生产螺钉和螺母的工人各多少名?设该车间每天有x人生产螺钉,则根据题意列出的方程为_____.
相关试题

