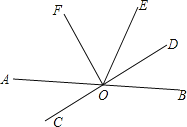
【题目】如图,直线AB与CD相交于点O,OD平分∠BOE,∠FOD=90°,问OF是∠AOE的平分线吗?请你补充完整小红的解答过程.
探究:
(1)当∠BOE=70°时,
∠BOD=∠DOE=![]() ,
,
∠EOF=90°﹣∠DOE= °,
而∠AOF+∠FOD+∠BOD=180°,
所以∠AOF+∠BOD=180°﹣∠FOD=90°,
所以∠AOF=90°﹣∠BOD= °,
所以∠EOF=∠AOF,OF是∠AOE的平分线.
(2)参考上面(1)的解答过程,请你证明,当∠BOE为任意角度时,OF是∠AOE的平分线.
(3)直接写出与∠AOF互余的所有角.
参考答案:
【答案】(1)55;55;(2)见解析;(3)与∠AOF互余的角有:∠AOC,∠BOD,∠DOE.
【解析】
试题分析:(1)根据题意、结合图形填空即可;
(2)根据角平分线的定义和余角的性质证明∠AOF=∠FOE,证明结论;
(3)根据余角的定义解答即可.
解:(1)当∠BOE=70°时,
∠BOD=∠DOE=![]() ,
,
∠EOF=90°﹣∠DOE=55°,
而∠AOF+∠FOD+∠BOD=180°,
所以∠AOF+∠BOD=180°﹣∠FOD=90°,
所以∠AOF=90°﹣∠BOD=55°,
所以∠EOF=∠AOF,OF是∠AOE的平分线,
故答案为:55;55;
(2)∵OD平分∠BOE,
∴∠BOD=∠DOE=![]() ∠BOE,
∠BOE,
∵∠FOD=90°,
∴∠AOF+∠BOD=90°,∠EOF+∠EOD=90°,
∴∠AOF=∠FOE,即OF是∠AOE的平分线;
(3)与∠AOF互余的角有:∠AOC,∠BOD,∠DOE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,垂足为E,且AB=6cm,则△DEB的周长为( )

A. 4cm B. 6cm C. 8cm D. 10cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+bx+c的图象过点(4,3)、(3,0).
(1)求b、c的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在下图中作出此二次函数的图象,根据图象说明,当x取何值时,y<0?

-
科目: 来源: 题型:
查看答案和解析>>【题目】先观察,再解答.
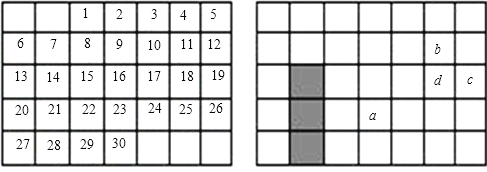
如图(1)是生活中常见的月历,你对它了解吗?
(1)图(2)是另一个月的月历,a表示该月中某一天,b、c、d是该月中其它3天,b、c、d与a有什么关系?b= ;c= ;d= .(用含a的式子填空).
(2)用一个长方形框圈出月历中的三个数字(如图3﹣2﹣2 (2)中的阴影),如果这三个数字之和等于51,这三个数字各是多少?
(3)这样圈出的三个数字的和可能是64吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设[x]表示不超过x的最大整数,如[2.7] =2,[-4.5] =-5;计算[3.7] + [-6.5] 的值为( )
A.-2 B.-3C.-4D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果上升3米记作3,那么下降3米记作米 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
相关试题

