【题目】有一块矩形地块![]() ,
,![]() 米,
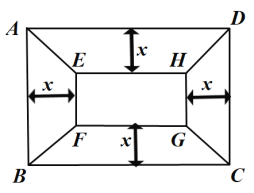
米,![]() 米,为美观,拟种植不同的花卉,如图所示,将矩形
米,为美观,拟种植不同的花卉,如图所示,将矩形![]() 分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为
分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为![]() 米.现决定在等腰梯形
米.现决定在等腰梯形![]() 和
和![]() 中种植甲种花卉;在等腰梯形
中种植甲种花卉;在等腰梯形![]() 和
和![]() 中种植乙种花卉;在矩形
中种植乙种花卉;在矩形![]() 中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米
中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米![]() 、60 元/米
、60 元/米![]() 、40元/米
、40元/米![]() ,设三种花卉的种植总成本为
,设三种花卉的种植总成本为![]() 元.
元.
(1)当![]() 时,求种植总成本
时,求种植总成本![]() ;
;
(2)求种植总成本![]() 与
与![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)若甲、乙两种花卉的种植面积之差不超过120米![]() ,求三种花卉的最低种植总成本.
,求三种花卉的最低种植总成本.
【答案】(1)当![]() 时,
时,![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() 最小为21600.
最小为21600.
【解析】
(1)根据![]() ,即可求解;
,即可求解;
(2)参考(1),由题意得:![]() ;
;
(3)![]() ,
,![]() ,则
,则![]() ,即可求解.
,即可求解.
解:(1)当![]() 时,
时,![]() ,
,![]() ,
,
故![]()
![]() ;
;
(2)![]() ,
,![]() ,参考(1),由题意得:
,参考(1),由题意得:![]() ;
;
(3)![]() ,
,
同理![]() ,
,
![]() 甲、乙两种花卉的种植面积之差不超过120米
甲、乙两种花卉的种植面积之差不超过120米![]() ,
,
![]() ,
,
解得:![]() ,
,
故![]() ,
,
而![]() 随
随![]() 的增大而减小,故当
的增大而减小,故当![]() 时,
时,![]() 的最小值为21600,
的最小值为21600,
即三种花卉的最低种植总成本为21600元.

