【题目】在矩形![]() 中,
中,![]() ,将其沿对角线
,将其沿对角线![]() 折叠,顶点
折叠,顶点![]() 的对应点
的对应点![]() ,
,![]() 交
交![]() 于点
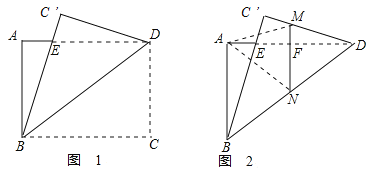
于点![]() 如图1,再折叠,使点
如图1,再折叠,使点![]() 落在
落在![]() 处,折痕
处,折痕![]() 交
交![]() 于
于![]() ,交
,交![]() 于
于![]() ,交
,交![]() 于
于![]() ,得到图2,则折痕
,得到图2,则折痕![]() 的长为____________.
的长为____________.
【答案】![]()
【解析】
由折叠的性质可知△DFM为直角三角形,且DF=![]() AD=2,可证△ABE≌△
AD=2,可证△ABE≌△![]() DE,在Rt△ABE中,由勾股定理求BE,利用△ABE∽△FDM,可得对应边的比相等可求MF,继而求出MN的长.
DE,在Rt△ABE中,由勾股定理求BE,利用△ABE∽△FDM,可得对应边的比相等可求MF,继而求出MN的长.
解:如图,由已知可得MN垂直平分AD,DF=![]() AD=2,FN=
AD=2,FN=![]() AB=
AB=![]() ,
,
∵AB=CD=![]() D,∠A=∠
D,∠A=∠![]() =90°,∠AEB=∠
=90°,∠AEB=∠![]() ED,
ED,
∴△ABE≌△![]() DE,∴BE=ED, ∠ABE=∠
DE,∴BE=ED, ∠ABE=∠![]() DE
DE
设AE=x,则BE=ED=4-x,
在Rt△ABE中,由勾股定理得
AB2+AE2=BE2,即32+x2=(4-x)2,
解得x=![]() ,∴AE=
,∴AE=![]()
∵∠ABE=∠![]() DE, ∠BAE=∠
DE, ∠BAE=∠![]() =90°,
=90°,
∴△ABE∽△FDM,
∴![]() =
=![]() ,即
,即 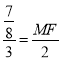 ,
,
解得MF=![]() .
.
∴MN=NF+FM=![]() +
+![]() =
=![]() .
.
故答案为:![]() .
.

