【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.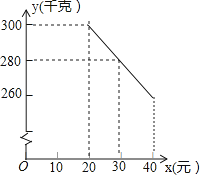
(1)求y与x的函数解析式(也称关系式)
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
参考答案:
【答案】
(1)
解:设y与x的函数关系式为y=kx+b,
根据题意,得: ![]() ,
,
解得: ![]() ,
,
∴y与x的函数解析式为y=﹣2x+340,(20≤x≤40)
(2)
解:由已知得:W=(x﹣20)(﹣2x+340)
=﹣2x2+380x﹣6800
=﹣2(x﹣95)2+11250,
∵﹣2<0,
∴当x≤95时,W随x的增大而增大,
∵20≤x≤40,
∴当x=40时,W最大,最大值为﹣2(40﹣95)2+11250=5200元
【解析】(1)待定系数法求解可得;(2)根据:总利润=每千克利润×销售量,列出函数关系式,配方后根据x的取值范围可得W的最大值.
本题主要考查待定系数法求一次函数解析式与二次函数的应用,根据相等关系列出函数解析式,并由二次函数的性质确定其最值是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.
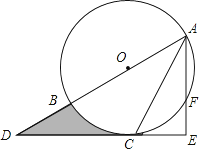
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图O是边长为9的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于点F,OE∥AC,交BC于点E,则OD+OE+OF的值为( )
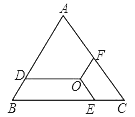
A. 3 B. 6 C. 8 D. 9
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一列按一定顺序和规律排列的数:
第一个数是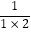 ;
;
第二个数是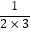 ;
;
第三个数是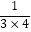 ;
;
…
对任何正整数n,第n个数与第(n+1)个数的和等于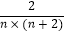 .
.
(1)经过探究,我们发现: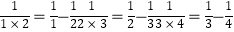
设这列数的第5个数为a,那么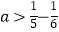 ,
, 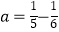 ,
,  ,哪个正确?
,哪个正确?
请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第n个数(即用正整数n表示第n数),并且证明你的猜想满足“第n个数与第(n+1)个数的和等于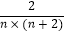 ”;
”;
(3)设M表示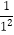 ,
, 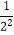 ,
, 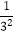 ,…,
,…, 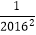 ,这2016个数的和,即
,这2016个数的和,即 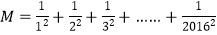 ,
,
求证: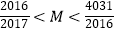 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在△ABC中,AH⊥BC,垂足为点H,若AB+BH=CH,∠ABH=70°,则∠BAC=_____°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABO中,AB⊥OB,OB=
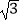 ,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( )
,AB=1,把△ABO绕点O旋转150°后得到△A1B1O,则点A1坐标为( ) 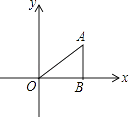
A.(﹣1,﹣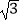 )
)
B.(﹣1,﹣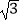 )或(﹣2,0)
)或(﹣2,0)
C.(﹣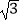 ,1)或(0,﹣2)
,1)或(0,﹣2)
D.(﹣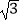 ,1)
,1)
相关试题

