【题目】为执行中央“节能减排,美化环境,建设美丽新农村”的国策,我市某村计划建造A、B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积、使用农户数及造价见下表:
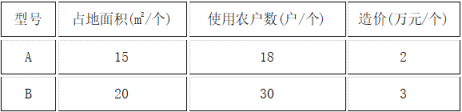
已知可供建造沼气池的占地面积不超过370m2,该村农户共有498户.
(1)满足条件的方案共有哪几种?写出解答过程.
(2)通过计算判断,哪种建造方案最省钱?造价最低是多少万元?
参考答案:
【答案】(1)方案共三种:分别是A型6个,B型14;A型7个,B型13个;A型8个,B型12个;(2)A型建8个的方案最省,最低造价52万元.
【解析】
(1)首先依据题意得出不等关系即可供建造垃圾初级处理点占地面积≤等于370m2,居民楼的数量大于等于498幢,由此列出不等式组,从而解决问题;
(2)本题可根据题意求出总费用为y与A型处理点的个数x之间的函数关系,从而根据一次函数的增减性来解决问题.
(1)设A型的建造了x个,
得不等式组:![]() ,
,
解得:6≤x≤8.5,
方案共三种:分别是A型6个,B型14;A型7个,B型13个;A型8个,B型12个;
(2)当x=6时,造价为2×6+3×14=54,
当x=7时,造价为2×7+3×13=53,
当x=8时,造价为2×8+3×12=52,
故A型建8个的方案最省,最低造价52万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】LED灯具有环保节能、投射范围大、无频闪、使用寿命较长等特点,在日常生活中,人们更倾向于LED灯的使用,某校数学兴趣小组为了解LED灯泡与普通白炽灯泡的销售情况,进行了市场调查:某商场购进一批30瓦的LED灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED灯泡
普通白炽灯泡
进价(元)
45
25
标价(元)
60
30

(1)该商场购进了LED灯泡与普通白炽灯泡共300个,LED灯泡按标价进行销售,而普通白炽灯泡打九折销售,当销售完这批灯泡后可以获利3200元,求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的30%,并求出此时这批灯泡的总利润为多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.
(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形:
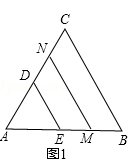
(1)当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由;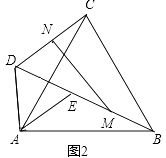
(2)当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论).
-
科目: 来源: 题型:
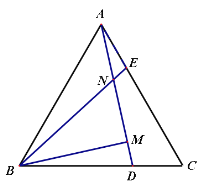
查看答案和解析>>【题目】已知:△ABC为等边三角形,点D、E分别在BC和AC上,并且CD=AE,连接AD、BE相交于点N,过点B作BM⊥AD于点M.
(1)求证:BE=AD
(2)若NE=2,MN=5,求AD的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某公园里一处矩形风景欣赏区ABCD,长AB=50米,宽BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为( )

A.100米 B.99米 C.98米 D.74米
-
科目: 来源: 题型:
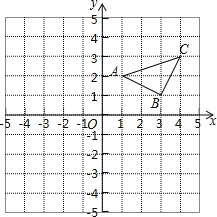
查看答案和解析>>【题目】已知:如图,在平面直角坐标系中,
(1) 作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1三个顶点的坐标:
A1 ,B1 ,C1 .
(2) 直接写出△ABC的面积为 .
(3) 在x轴上画点P,使△PAC的周长最小. (不写作法,保留作图痕迹)
相关试题

