Question

【题目】如图①，现有一张三角形ABC纸片，沿BC边上的高AE所在的直线翻折，使得点C与BC边上的点D重合．

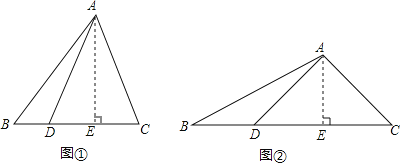
（1）填空：△ADC是 三角形；

（2）若AB=15，AC=13，BC=14，求BC边上的高AE的长；

（3）如图②，若∠DAC=90°，试猜想：BC、BD、AE之间的数量关系，并加以证明．

Answer 1

【答案】（1）等腰（2）12（3）见解析

【解析】

试题分析：（1）根据折叠得到AD=AC，所以△ADC是等腰三角形；

（2）设CE=x，利用勾股定理得到方程132﹣x2=152﹣（14﹣x）2解得：x=5，在Rt△AEC中，由勾股定理即可解答；

（3）猜想BC、BD、AE之间的数量关系为：BC﹣BD=2AE．由△ADC是等腰三角形，又∠DAC=90°，得到△ADC是等腰直角三角形又AE是CD边上的高，所以△AED与△AEC都是等腰直角三角形，即可得到CD=2AE．由BC﹣BD=CD，即可解答．

解：（1）∵三角形ABC纸片，沿BC边上的高AE所在的直线翻折，使得点C与BC边上的点D重合．

∴AD=AC，

∴△ADC是等腰三角形；

故答案为：等腰．

（2）设CE=x，则BE=14﹣x，

在Rt△AEC中，由勾股定理得：AE2=AC2﹣CE2，

∴AE2=132﹣x2

在Rt△ABE中，由勾股定理得：AE2=AB2﹣BE2，

∴AE2=152﹣（14﹣x）2

∴132﹣x2=152﹣（14﹣x）2

解得：x=5，

在Rt△AEC中，由勾股定理得：．

（3）猜想BC、BD、AE之间的数量关系为：BC﹣BD=2AE．

证明如下：

由（1）得：△ADC是等腰三角形，又∠DAC=90°，

∴△ADC是等腰直角三角形

又AE是CD边上的高，

∴DE=CE，，

∴△AED与△AEC都是等腰直角三角形，

∴DE=AE=EC，即CD=2AE．

∵BC﹣BD=CD

∴BC﹣BD=2AE．