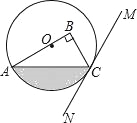
【题目】如图，在Rt△ABC中，∠B=90°，点O在边AB上，以点O为圆心，OA为半径的圆经过点C，过点C作直线MN，使∠BCM=2∠A．

（1）判断直线MN与⊙O的位置关系，并说明理由；

（2）若OA=4，∠BCM=60°，求图中阴影部分的面积．

参考答案：

【答案】(1) MN是⊙O切线，理由详见解析；（2）．

【解析】

试题分析：（1）MN是⊙O切线，只要证明∠OCM=90°即可．（2）求出∠AOC以及BC，根据S阴=S扇形OAC﹣S△OAC计算即可．

试题解析：（1）MN是⊙O切线．

理由：连接OC．

∵OA=OC，

∴∠OAC=∠OCA，

∵∠BOC=∠A+∠OCA=2∠A，∠BCM=2∠A，

∴∠BCM=∠BOC，

∵∠B=90°，

∴∠BOC+∠BCO=90°，

∴∠BCM+∠BCO=90°，

∴OC⊥MN，

∴MN是⊙O切线．

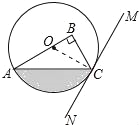
（2）由（1）可知∠BOC=∠BCM=60°，

∴∠AOC=120°，

在RT△BCO中，OC=OA=4，∠BCO=30°，

∴BO=OC=2，BC=2

∴S阴=S扇形OAC﹣S△OAC= ．

关闭