【题目】如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
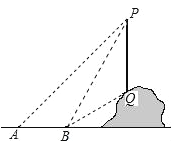
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m).备用数据:![]() ,
,![]() .
.
参考答案:
【答案】(1)30°;(2)9米.
【解析】
试题分析:(1)延长PQ交直线AB于点E,根据直角三角形两锐角互余求得即可;
(2)设PE=x米,在直角△APE和直角△BPE中,根据三角函数利用x表示出AE和BE,根据AB=AE-BE即可列出方程求得x的值,再在直角△BQE中利用三角函数求得QE的长,则PQ的长度即可求解.
试题解析:延长PQ交直线AB于点E,
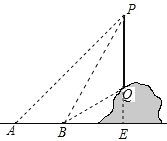
(1)∠BPQ=90°-60°=30°;
(2)设PE=x米.
在直角△APE中,∠A=45°,
则AE=PE=x米;
∵∠PBE=60°
∴∠BPE=30°
在直角△BPE中,BE=![]() PE=
PE=![]() x米,
x米,
∵AB=AE-BE=6米,
则x-![]() x=6,
x=6,
解得:x=9+3![]() .
.
则BE=(3![]() +3)米.
+3)米.
在直角△BEQ中,QE=![]() BE=
BE=![]() (3
(3![]() +3)=(3+
+3)=(3+![]() )米.
)米.
∴PQ=PE-QE=9+3![]() -(3+
-(3+![]() )=6+2
)=6+2![]() ≈9(米).
≈9(米).
答:电线杆PQ的高度约9米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
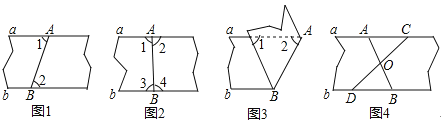
A.如图1,展开后测得∠1=∠2
B.如图2,展开后测得∠1=∠2且∠3=∠4
C.如图3,测得∠1=∠2
D.如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
-
科目: 来源: 题型:
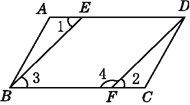
查看答案和解析>>【题目】如图,已知AD∥BC,∠1=∠2,要说明∠3+∠4=180°,请补充完整解题过程,并在括号内填上相应的依据:
解:因为AD∥BC(已知),
所以∠1=∠3(__________________________________).
因为∠1=∠2(已知),
所以∠2=∠3.
所以BE∥__________ (______________________________________).
所以∠3+∠4=180°(______________________________________).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴正半轴上,反比例函数y=
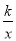 (x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .
(x>0)的图象经过该菱形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8),则点F的坐标是 .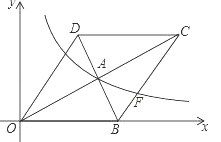
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图.
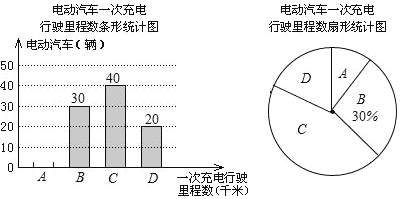
根据以上信息,解答下列问题:
(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图;
(2)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形具有稳定性的是( )
A.正方形 B.矩形 C.平行四边形 D.直角三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值已知A=x2-2x-1, B=2x2-6x+3, 求3A-[(2A-B)-2(A-B)]的值,其中x=-7.
相关试题

