【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(6,4),E为AB的中点,过点D(8,0)和点E的直线分别与BC、y轴交于点F、G.

(1)求直线DE的函数关系式;
(2)函数y=mx﹣2的图象经过点F且与x轴交于点H,求出点F的坐标和m值;
(3)在(2)的条件下,求出四边形OHFG的面积.
参考答案:
【答案】(1)直线DE的函数关系式为:y=﹣x+8;(2)点F的坐标为;(4,4);m=![]() ;(3)18
;(3)18![]() .
.
【解析】
试题分析:(1)由顶点B的坐标为(6,4),E为AB的中点,可求得点E的坐标,又由过点D(8,0),利用待定系数法即可求得直线DE的函数关系式;
(2)由(1)可求得点F的坐标,又由函数y=mx﹣2的图象经过点F,利用待定系数法即可求得m值;
(3)首先可求得点H与G的坐标,即可求得CG,OC,CF,OH的长,然后由S四边形OHFG=S梯形OHFC+S△CFG,求得答案.
解:(1)设直线DE的解析式为:y=kx+b,
∵顶点B的坐标为(6,4),E为AB的中点,
∴点E的坐标为:(6,2),
∵D(8,0),
∴![]() ,
,
解得:![]() ,
,
∴直线DE的函数关系式为:y=﹣x+8;
(2)∵点F的纵坐标为4,且点F在直线DE上,
∴﹣x+8=4,
解得:x=4,
∴点F的坐标为;(4,4);
∵函数y=mx﹣2的图象经过点F,
∴4m﹣2=4,
解得:m=![]() ;
;
(3)由(2)得:直线FH的解析式为:y=![]() x﹣2,
x﹣2,
∵![]() x﹣2=0,
x﹣2=0,
解得:x=![]() ,
,
∴点H(![]() ,0),
,0),
∵G是直线DE与y轴的交点,
∴点G(0,8),
∴OH=![]() ,CF=4,OC=4,CG=OG﹣OC=4,
,CF=4,OC=4,CG=OG﹣OC=4,
∴S四边形OHFG=S梯形OHFC+S△CFG=![]() ×(
×(![]() +4)×4+
+4)×4+![]() ×4×4=18
×4×4=18![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠C=90°,BE平分∠ABC,DF平分∠ADC,则BE与DF有何位置关系?试说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有四张正面分别标有﹣1,0,1,2的不透明卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中取出一张,将卡片上的数字记为a,不放回,再取出一张,将卡片上的数字记为b,设P点的坐标为(a,b).如图,点P落在抛物线y=x2与直线y=x+2所围成的封闭区域内(图中含边界的阴影部分)的概率是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BC相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长.
-
科目: 来源: 题型:
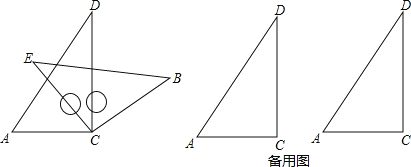
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=45°,则∠ACB的度数为 ;
②若∠ACB=140°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)当∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为庆祝战胜利70周年,我市某楼盘让利于民,决定将原价为a元/米2的商品房价降价10%销售,降价后的销售价为( )
A.a-10% B.a10%
C.a(1-10%) D.a(1+10%)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中,是命题的是( )
A. 直线AB和CD垂直吗 B. 过线段AB的中点C画AB的垂线
C. 同旁内角不互补,两直线不平行 D. 连接A,B两点
相关试题

